【题目】如图,四边形ABCD中,AD∥BC,∠ADC=120°,P为直线CD上一动点,点M在线段BC上,连MP,设∠MPD=α.
(1)如图1,若MP⊥CD,则∠BMP=___度;
(2)如图2,当P点在CD延长线上时,∠BMP=___(用α表示);
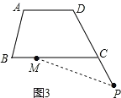
(3)如图3,当P点在DC延长线上时,(2)中结论是否仍成立?请画出图形并证明你的判断.

参考答案:
【答案】(1)150;(2)60°+α;(3)不成立.理由见解析.
【解析】
(1)根据两直线平行,同旁内角互补求出∠C,然后利用三角形的内角和定理求出∠CMP,再根据平角的定义列式计算即可得解;
(2)根据两直线平行,同旁内角互补求出∠C,然后利用三角形的内角和定理求出∠CMP,再根据平角的定义列式计算即可得解;
(3)根据两直线平行,同位角相等∠BCP,然后利用三角形的内角和定理求出∠CMP,再根据平角的定义列式计算即可得解.
解:(1)∵AD∥BC,
∴∠C=180°-∠ADC=180°-120°=60°,
∵MP⊥CD,
∴∠CMP=90°-∠C=90°-60°=30°,
∴∠BMP=180°-∠CMP=180°-30°=150°;
(2)∵AD∥BC,
∴∠C=180°-∠ADC=180°-120°=60°,
在△CMP中,∠CMP=180°-∠C-∠MPD=180°-60°-α=120°-α,
∴∠BMP=180°-∠CMP=180°-(120°-α)=60°+α;
(3)不成立.
理由如下:∵AD∥BC,
∴∠BCP=∠ADC=120°,
在△CMP中,∠CMP=180°-∠BCP-∠MPD=180°-120°-α=60°-α,
∴∠BMP=180°-∠CMP=180°-(60°-α)=120°+α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣1,﹣1),B(3,2),C(1,4)
(1)画出△ABC向上平移2个单位,向左平移3个位置后的△A′B′C′;
(2)写出A、C的对应点A′、C′的坐标;
(3)求两次平移过程中线段AC扫过的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AF∥DE,B为AF上一点,∠ABC=60°,交ED于C,CM平分∠BCE,∠MCN=90°.
(1)求∠DCN的度数;
(2)若∠CBF的平分线交CN于N,求证:BN∥CM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O(0,0),B(2,3),点A在坐标轴上,且S△AOB=6.
(1)求满足条件的点A的坐标;
(2)点C(﹣3,1),过O点直线l把三角形BOC分成面积相等的两部分,交BC于D,则D的坐标为 .

-
科目: 来源: 题型:
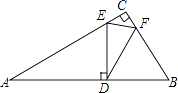
查看答案和解析>>【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E,F分别在AC,BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= .
-
科目: 来源: 题型:
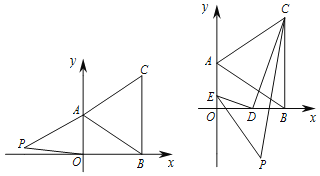
查看答案和解析>>【题目】在下面直角坐标系中,已知A(0,a)、B(b,0)、C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0.
(1)a= ;b= ;c= ;
(2)在第二象限内,是否存在点P(m,
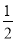 ),使四边形ABOP的面积与△ABC的面积相等?若存在,求出点m的值;若不存在,请说明理由;
),使四边形ABOP的面积与△ABC的面积相等?若存在,求出点m的值;若不存在,请说明理由;(3)D为线段OB上一动点,连接CD,过D作DE⊥CD交y轴于点E,EP、CP分别平分∠DEO和∠DCB,当点D在OB上运动的过程中,∠P的度数是否变化,若不变,请求出∠P的度数;若变化,请说明理由.
相关试题

