【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E,F分别在AC,BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= . 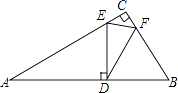
参考答案:
【答案】![]() 或
或 ![]()
【解析】解:∵∠EDF=30°,ED⊥AB于D,
∴∠FDB=∠B=60°,
∴△BDF是等边三角形;
∵BC=1,∴AB=2;
∵BD=BF,
∴2﹣AD=1﹣CF;
∴AD=CF+1.
①如图1,∠FED=90°,△CEF∽△EDF,
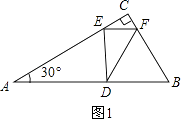
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,CF= ![]() ;
;
∴AD= ![]() +1=
+1= ![]() ;
;
②如图2,∠EFD=90°,△CEF∽△FED,
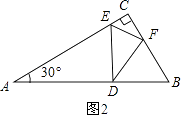
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ;
;
解得,CF= ![]() ;
;
∴AD= ![]() +1=
+1= ![]() .
.
故答案为 ![]() 或
或 ![]() .
.
由于∠EDF=30°,且DE总垂直于AB,因此∠FDB=60°,从而得出△FDB是等边三角形,故BD=BF,2-AD=1-CF,即AD=CF+1.由于∠C是直角,当△CEF∽△DEF时,△DEF必为直角三角形,那么可分两种情况讨论:①∠DEF=90°,此时,△CEF∽△DEF;②∠DFE=90°,此时△CEF∽△FED;可根据各相似三角形得到的比例线段求出CF的值,进而可求得AD的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AF∥DE,B为AF上一点,∠ABC=60°,交ED于C,CM平分∠BCE,∠MCN=90°.
(1)求∠DCN的度数;
(2)若∠CBF的平分线交CN于N,求证:BN∥CM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O(0,0),B(2,3),点A在坐标轴上,且S△AOB=6.
(1)求满足条件的点A的坐标;
(2)点C(﹣3,1),过O点直线l把三角形BOC分成面积相等的两部分,交BC于D,则D的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,∠ADC=120°,P为直线CD上一动点,点M在线段BC上,连MP,设∠MPD=α.
(1)如图1,若MP⊥CD,则∠BMP=___度;
(2)如图2,当P点在CD延长线上时,∠BMP=___(用α表示);
(3)如图3,当P点在DC延长线上时,(2)中结论是否仍成立?请画出图形并证明你的判断.

-
科目: 来源: 题型:
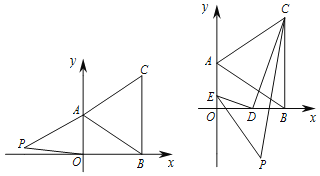
查看答案和解析>>【题目】在下面直角坐标系中,已知A(0,a)、B(b,0)、C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0.
(1)a= ;b= ;c= ;
(2)在第二象限内,是否存在点P(m,
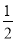 ),使四边形ABOP的面积与△ABC的面积相等?若存在,求出点m的值;若不存在,请说明理由;
),使四边形ABOP的面积与△ABC的面积相等?若存在,求出点m的值;若不存在,请说明理由;(3)D为线段OB上一动点,连接CD,过D作DE⊥CD交y轴于点E,EP、CP分别平分∠DEO和∠DCB,当点D在OB上运动的过程中,∠P的度数是否变化,若不变,请求出∠P的度数;若变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为打造书香校园,购进了甲、乙两种型号的新书柜来放置新买的图书,甲型号书柜共花了15000元,乙型号书柜共花了18000元,乙型号书柜比甲型号书柜单价便宜了300元,购买乙型号书柜的数量是甲型号书柜数量的2倍.求甲、乙型号书柜各购进多少个?
相关试题

