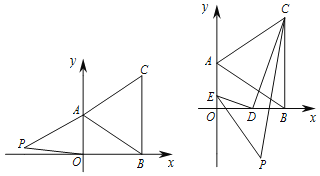
【题目】在下面直角坐标系中,已知A(0,a)、B(b,0)、C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0.
(1)a= ;b= ;c= ;
(2)在第二象限内,是否存在点P(m,![]() ),使四边形ABOP的面积与△ABC的面积相等?若存在,求出点m的值;若不存在,请说明理由;
),使四边形ABOP的面积与△ABC的面积相等?若存在,求出点m的值;若不存在,请说明理由;
(3)D为线段OB上一动点,连接CD,过D作DE⊥CD交y轴于点E,EP、CP分别平分∠DEO和∠DCB,当点D在OB上运动的过程中,∠P的度数是否变化,若不变,请求出∠P的度数;若变化,请说明理由.
参考答案:
【答案】(1)2,3,4;(2)存在,m=﹣3;(3)∠P的度数不变,∠P=45°,理由见解析
【解析】
(1)根据非负数的性质解答即可;
(2)根据四边形ABOP的面积=△ABO的面积+△APO的面积可得关于m的方程,解方程即得答案;
(3)易得BC∥y轴,过点P作PF∥BC,过点D作DM∥BC,易证∠P=∠OEP+∠PCB,∠EDC=∠OED+∠DCB,则可得∠P=![]() ∠EDC,进而可得结论.
∠EDC,进而可得结论.
解:(1)∵|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0,
∴a﹣2=0,b﹣3=0,c﹣4=0,
解得:a=2,b=3,c=4;
故答案为:2;3;4.
(2)∵a=2,b=3,c=4,
∴A(0,2),B(3,0),C(3,4),
∴OA=2,OB=3,
∵S△ABO=![]() ×2×3=3,S△APO=
×2×3=3,S△APO=![]() ×2×(﹣m)=﹣m,
×2×(﹣m)=﹣m,
∴S四边形ABOP=S△ABO+S△APO=3+(﹣m)=3﹣m.
∵S△ABC=![]() ×4×3=6,
×4×3=6,
∴S四边形ABOP=S△ABC=3﹣m=6,
∴m=﹣3,
∴存在点P(﹣3,![]() ),使S四边形ABOP=S△ABC.
),使S四边形ABOP=S△ABC.
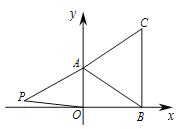
(3)∠P的度数不变,∠P=45°,理由如下:
∵B(b,0)、C(b,c)的横坐标相同,
∴BC∥y轴,
过点P作PF∥BC,如图,

∴PF∥y轴,
∴∠OEP=∠EPF,∠PCB=∠FPC,
∴∠EPC=∠EPF+∠FPC=∠OEP+∠PCB,
过点D作DM∥BC,
同理可得∠EDC=∠OED+∠DCB,
∵EP、CP分别平分∠DEO和∠DCB,
∴∠OEP=![]() ∠OED,∠PCB=
∠OED,∠PCB=![]() ∠DCB,
∠DCB,
∴∠EPC=![]() =
=![]() (∠OED+∠DCB)=
(∠OED+∠DCB)=![]() ∠EDC,
∠EDC,
∵DE⊥CD,∴∠EDC=90°,
∴∠EPC=![]() ×90°=45°.
×90°=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,∠ADC=120°,P为直线CD上一动点,点M在线段BC上,连MP,设∠MPD=α.
(1)如图1,若MP⊥CD,则∠BMP=___度;
(2)如图2,当P点在CD延长线上时,∠BMP=___(用α表示);
(3)如图3,当P点在DC延长线上时,(2)中结论是否仍成立?请画出图形并证明你的判断.

-
科目: 来源: 题型:
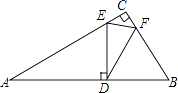
查看答案和解析>>【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E,F分别在AC,BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为打造书香校园,购进了甲、乙两种型号的新书柜来放置新买的图书,甲型号书柜共花了15000元,乙型号书柜共花了18000元,乙型号书柜比甲型号书柜单价便宜了300元,购买乙型号书柜的数量是甲型号书柜数量的2倍.求甲、乙型号书柜各购进多少个?
-
科目: 来源: 题型:
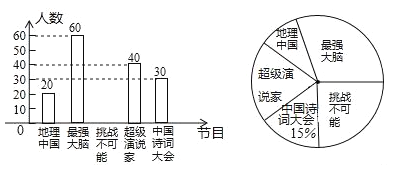
查看答案和解析>>【题目】我市某中学为了了解孩子们对《中国诗词大会》、《挑战不可能》、《最强大脑》、《超级演说家》、《地理中国》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题:
(1)本次调查中共抽取了 名学生.
(2)补全条形统计图.
(3)在扇形统计图中,喜爱《地理中国》节目的人数所在的扇形的圆心角是 度.
-
科目: 来源: 题型:
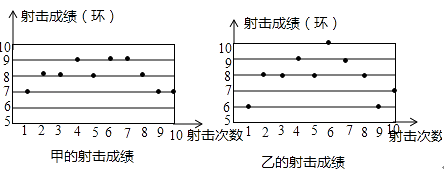
查看答案和解析>>【题目】如图是一次射击训练中甲、乙两人的10次射击成绩的分布情况,则射击成绩的方差较小的是(填“甲”或“乙”).
相关试题

