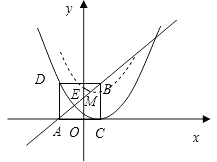
【题目】如图，已知点B（1，3），C（1，0），直线y=x+k经过点B，且与x轴交于点A，将△ABC沿直线AB折叠得到△ABD．

（1）填空：A点坐标为（ ， ），D点坐标为（ ， ）；
（2）若抛物线y= x2+bx+c经过C，D两点，求抛物线的解析式；
（3）将（2）中的抛物线沿y轴向上平移，设平移后所得抛物线与y轴交点为E，点M是平移后的抛物线与直线AB的公共点，在抛物线平移过程中是否存在某一位置使得直线EM∥x轴．若存在，此时抛物线向上平移了几个单位？若不存在，请说明理由．
（提示：抛物线y=ax2+bx+c（a≠0）的对称轴是x=﹣ ，顶点坐标是（﹣ ， ）

参考答案：

【答案】
（1）﹣2；0；﹣2；3
（2）

解：∵抛物线y= x2+bx+c经过C（1，0），D（﹣2，3）代入，解得：b=﹣ ，c=

∴所求抛物线解析式为：y= x2﹣ x+ ；


（3）

解：答：存在．

∵当点M在抛物线对称轴的左侧或在抛物线的顶点时，仅当M，E重合时，它们的纵坐标相等．

∴EM不会与x轴平行，

当点M在抛物线的右侧时，

设抛物线向上平移H个单位能使EM∥x轴，

则平移后的抛物线的解析式为

∵y= （x﹣1）2+h，

∴抛物线与y轴交点E（0， +h），

∵抛物线的对称轴为：x=1，

根据抛物线的对称性，可知点M的坐标为（2， +h）时，直线EM∥x轴，

将（2， +h）代入y=x+2得 +h=2+2

解得：h= ．

∴抛物线向上平移 个单位能使EM∥x轴．


【解析】解：（1）A（﹣2，0），D（﹣2，3）
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点，以及对二次函数的性质的理解，了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．

关闭