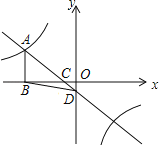
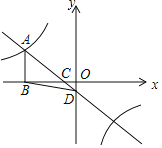
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(1)求一次函数和反比例函数的解析式;
(2)若直线AC与y轴交于点D,求△BCD的面积.
参考答案:
【答案】(1)反比例函数的解析式为y=﹣![]() ,一次函数的解析式为y=﹣
,一次函数的解析式为y=﹣![]() x﹣
x﹣![]() ;(2)S△BCD=1.
;(2)S△BCD=1.
【解析】
(1)根据点A坐标,点C坐标,结合△ABC的面积是3,求出m的值,从而确定点A的坐标,利用待定系数法即可求出反比例函数解析式,一次函数解析式;
(2)求出点D坐标,利用三角形面积公式进行求解即可得.
(1)∵AB⊥x轴于点B,点A(m,2),∴点B(m,0),AB=2,
∵点C(﹣1,0),∴BC=﹣1﹣m,
∴S△ABC=![]() ABBC=﹣1﹣m=3,∴m=﹣4,∴点A(﹣4,2),
ABBC=﹣1﹣m=3,∴m=﹣4,∴点A(﹣4,2),
∵点A在反比例函数y=![]() (a≠0)的图象上,∴a=﹣4×2=﹣8,
(a≠0)的图象上,∴a=﹣4×2=﹣8,
∴反比例函数的解析式为y=﹣![]() ,
,
将A(﹣4,2)、C(﹣1,0)代入y=kx+b,得:
![]() ,解得:
,解得: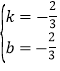 ,∴一次函数的解析式为y=﹣
,∴一次函数的解析式为y=﹣![]() x﹣
x﹣![]() ;
;
(2)当x=0时,y=﹣![]() x﹣
x﹣![]() =﹣
=﹣![]() ,
,
∴点D(0,﹣![]() ),
),
∴OD=![]() ,
,
∴S△BCD=![]() BCOD=
BCOD=![]() ×3×
×3×![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:
在△ABC中,AB,BC,AC三边的长度分别为
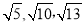 ,求这个三角形的面积。
,求这个三角形的面积。小辉同学在解得这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.

(1)请你直接写出△ABC的面积为:______;
思维拓展
(2)若△DEF三边的长分别为
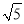 a,2
a,2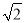 a,
a,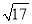 a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;探索创新:
(3)若在△ABC三边的长分别为
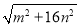 ,
,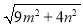 ,
,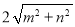 (m>0,n>0,且m≠n),试运用构图法求出三角形的面积。
(m>0,n>0,且m≠n),试运用构图法求出三角形的面积。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC, ∠BAC=90°,D是斜边BC的中点,E,F分别是AB,AC边上的点,且DE⊥DF.
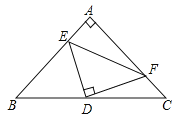
(1)判断DE和DF的数量关系,并说明理由;
(2)若BE=12,CF=5,求△DEF的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)9
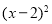 (3x2)(3x2)
(3x2)(3x2)(2)(1
 x)2(1
x)2(1 x)2
x)2(3)(a2b1)(a2b1)
(4)
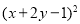
-
科目: 来源: 题型:
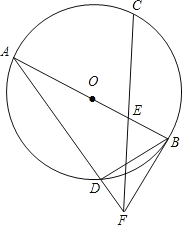
查看答案和解析>>【题目】如图,AB是⊙O的直径,
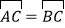 ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.(1)求证:直线BF是⊙O的切线;
(2)若OB=2,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)
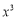 yx
yx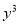 ;
;(2)(x2)(x4)+
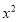 -4.
-4.(3)(x24y2)216x2y2
(4)(p4)(p1)6.
相关试题

