【题目】因式分解:
(1)![]() yx
yx![]() ;
;
(2)(x2)(x4)+![]() -4.
-4.
(3)(x24y2)216x2y2
(4)(p4)(p1)6.
参考答案:
【答案】(1)xy(x+y)(xy)(2)2(x+2)(x+1)(3) (x2y)2(x-2y)2(4) (p2)(p-1)
【解析】
(1)首先提公因式xy,再利用平方差进行二次分解即可;
(2)首先把后两项利用平方差进行分解,再提公因式x+2,然后化简即可;
(3)先根据平方差公式进行因式分解,再根据完全平方公式即可求解;
(4)先根据整式的乘法进行运算,再根十字相乘法因式分解.
(1)![]() yx
yx![]()
=xy(x2y2),
=xy(x+y)(xy)
(2)(x2)(x4)+![]() -4.
-4.
=(x+2)(x+4)+(x+2)(x2),
=(x+2)(x+4+x2),
=(x+2)(2x+2),
=2(x+2)(x+1)
(3)(x24y2)216x2y2
=(x24y2+4xy) (x24y2-4xy)
=(x2y)2(x-2y)2
(4)(p4)(p1)6
=p2+p-4p-4+6
= p2-3p+2
=(p2)(p-1).
-
科目: 来源: 题型:
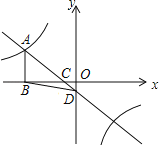
查看答案和解析>>【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=
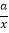 (a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.(1)求一次函数和反比例函数的解析式;
(2)若直线AC与y轴交于点D,求△BCD的面积.
-
科目: 来源: 题型:
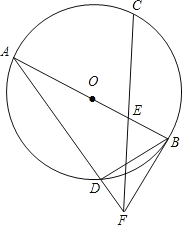
查看答案和解析>>【题目】如图,AB是⊙O的直径,
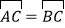 ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.(1)求证:直线BF是⊙O的切线;
(2)若OB=2,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由
(3)若|CF﹣AE|=2,EF=2
 ,当△POF为等腰三角形时,请直接写出线段OP的长.
,当△POF为等腰三角形时,请直接写出线段OP的长.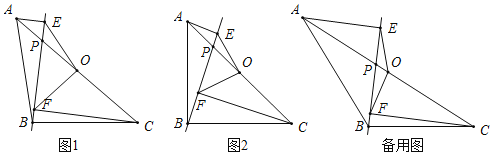
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算并观察下列各式:
(x1)(x1) ;
(x1)(
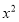 x1) ;
x1) ;(x1)(
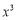
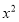 x1) ;
x1) ;(2)从上面的算式及计算结果,你发现了什么?请根据你发现的规律直接写下面的空格.(x1)
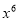 1;
1;(3)利用你发现的规律计算:
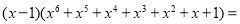 ;
;(4)利用该规律计算:
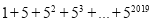 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入它所在的数集的括号里.
﹣
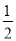 ,+5,﹣6.3,0,﹣
,+5,﹣6.3,0,﹣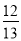 ,2
,2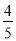 ,6.9,﹣7,210,0.031,﹣43,﹣10%
,6.9,﹣7,210,0.031,﹣43,﹣10%正数集合:{ …}
整数集合:{ …}
非负数集合:{ …}
负分数集合:{ …}.
相关试题

