【题目】如图,△ABC中,AB=AC, ∠BAC=90°,D是斜边BC的中点,E,F分别是AB,AC边上的点,且DE⊥DF.
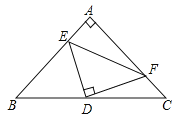
(1)判断DE和DF的数量关系,并说明理由;
(2)若BE=12,CF=5,求△DEF的面积。
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接AD,易证明△AED与△CFD全等,可得DE=DF
(2) ∵BE=12,CF=5,由△AED与△CFD全等可得AE=CF=5,AF=BE=12;在△AEF中,由勾股定理可得EF=13;在△DEF中,由勾股定理可得DE2=DF2;则△DEF的面积是亦可以求出
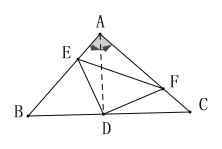
如图,连接AD,
∵AB=AC,D为BC中点
∴AD⊥BC,AD=CD=BD
又∵DE⊥DF
∴∠CDF+∠ADF=∠EDA+∠ADF
即∠CDF=∠ADE
在△DCF与△DAE中
∵∠CDF=∠ADE
∠C=∠DAE
CD=AD
∴△DCF![]() △DAE
△DAE
∴DF=DE
(2)由(1)得:AE=CF=5, AF=BE=12
∵∠EAF=90°
∴![]()
∴EF=13
又∵DE=DF,且DE⊥DF
∴![]()
∴DE=DF=![]()
∴![]() =
=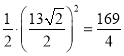
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE的外角平分线,CD与BD交于点D.
(1)若∠A=50°,则∠D= ;
(2)若∠A=80°,则∠D= ;
(3)若∠A=130°,则∠D= ;
(4)若∠D=36°,则∠A= ;
(5)综上所述,你会得到什么结论?证明你的结论的准确性.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句:①-1是1的平方根。②带根号的数都是无理数。③-1的立方根是-1。④
 的立方根是2。⑤(-2)2的算术平方根是2。⑥-125的立方根是±5。⑦有理数和数轴上的点一一对应。其中正确的有( )
的立方根是2。⑤(-2)2的算术平方根是2。⑥-125的立方根是±5。⑦有理数和数轴上的点一一对应。其中正确的有( )A. 2个B. 3个C. 4个D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:
在△ABC中,AB,BC,AC三边的长度分别为
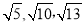 ,求这个三角形的面积。
,求这个三角形的面积。小辉同学在解得这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.

(1)请你直接写出△ABC的面积为:______;
思维拓展
(2)若△DEF三边的长分别为
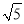 a,2
a,2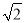 a,
a,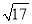 a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC. 并利用构图法求出它的面积;探索创新:
(3)若在△ABC三边的长分别为
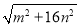 ,
,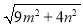 ,
,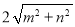 (m>0,n>0,且m≠n),试运用构图法求出三角形的面积。
(m>0,n>0,且m≠n),试运用构图法求出三角形的面积。 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)9
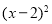 (3x2)(3x2)
(3x2)(3x2)(2)(1
 x)2(1
x)2(1 x)2
x)2(3)(a2b1)(a2b1)
(4)
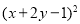
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=
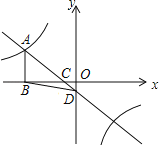
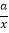 (a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.(1)求一次函数和反比例函数的解析式;
(2)若直线AC与y轴交于点D,求△BCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,
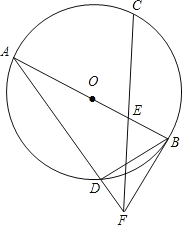
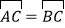 ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.(1)求证:直线BF是⊙O的切线;
(2)若OB=2,求BD的长.
相关试题

