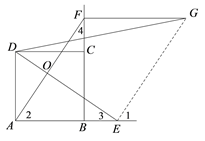
【题目】已知正方形ABCD,点E,F分别在射线AB,射线BC上,AE=BF,DE与AF交于点O.
(1)如图1,当点E,F分别在线段AB,BC上时,则线段DE与AF的数量关系是 ,位置关系是 .
(2)如图2,当点E在线段AB延长线上时,将线段AE沿AF进行平移至FG,连接DG.
①依题意将图2补全;
②小亮通过观察、实验提出猜想:在点E运动的过程中,始终有![]() .
.
小亮把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:连接EG,要证明![]() ,只需证四边形FAEG是平行四边形及△DGE是等腰直角三角形.
,只需证四边形FAEG是平行四边形及△DGE是等腰直角三角形.
想法2:延长AD,GF交于点H,要证明![]() ,只需证△DGH是直角三角形.
,只需证△DGH是直角三角形.

图1 图2
请你参考上面的想法,帮助小亮证明![]() .(一种方法即可)
.(一种方法即可)
参考答案:
【答案】(1)相等,垂直;(2)①补图见解析;②证明见解析
【解析】解:(1)相等,垂直..
(2)①依题意补全图形..
②法1:
证明:连接GE.
由平移可得AE=FG,AE∥FG,∴四边形AEGF是平行四边形.
∴AF=EG,AF∥EG,
∴∠1=∠2.
∵四边形ABCD是正方形,
∴AD = AB,∠DAE=∠ABC= 90°.
∵AE=BF,
∴△AED≌△BFA.
∴∠3=∠4,AF = DE.
∴EG=DE.
∵∠2+∠4=90°,
∴∠1+∠3=90°,∴∠DEG=90°.
∴![]() .
.
又 ∵![]() ,
,
∴![]() .
.
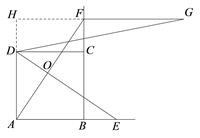
法2:
证明:延长AD,GF交于点H,
由平移可得AE=FG,AE∥FG,
∴∠H+∠DAB= 180°
∵四边形ABCD是正方形,
∴∠DAB= 90°,AD=DC.
∴∠H = 90°.
∴![]() .
.
∵∠HDC=∠DCF= 90°,
∴四边形HDCF是矩形.
∴HF=DC.
∴HF=AD.
∵HG=FG+HF,
∴HG=AE+HF=AE+AD.
∵易证BF=AH 且BF=AE,
∴HD=AE –AD.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
 与y轴交于点C,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为﹣1.
与y轴交于点C,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为﹣1.(1)求a的值;
(2)设抛物线的顶点P关于原点的对称点为P′,求点P′的坐标;
(3)将抛物线在A,B两点之间的部分(包括A,B两点),先向下平移 3个单位,再向左平移m(
 )个单位,平移后的图象记为图象G,若图象G与直线PP′ 无交点,求m的取值范围.
)个单位,平移后的图象记为图象G,若图象G与直线PP′ 无交点,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)(x+2)2-(x+5)(x-5),其中x=
 。
。(2)[(x+2y)2-(x+y)(3x-y)-5y2]÷2x,其中x=-2,y=
 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)求x的值:(x﹣1)2=25;
(2)计算: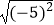 ﹣
﹣ 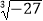 +
+ 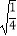 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过点C的切线,垂足为点D,AB的延长线交切线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB =4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为保证中小学生每天锻炼一小时,涟水县某中学开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的统计图(1)和图(2).

(1)某班同学的总人数为人;
(2)请根据所给信息在图(1)中将表示“乒乓球”项目的图形补充完整;
(3)扇形统计图(2)中表示“篮球”项目扇形的圆心角度数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是规格为8×8的正方形网格,每个小方格都是边长为1的正方形,请在所给网格中按下列要求操作:

(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4);
(2)在第二象限内的格点(网格线的交点)上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是;
(3)画出△ABC关于y轴对称的△A′B′C′.
相关试题

