【题目】如图,ABCD中,E为AD边的中点,把△ABE沿BE翻折,得到△FBE,连接DF并延长交BC于G. 
(1)求证:四边形BEDG为平行四边形.
(2)若BE=AD=10,且ABCD的面积等于60,求FG的长.
参考答案:
【答案】
(1)解:证明:∵把△ABE沿BE翻折,得到△FBE,
∴AE=EF,∠AEB=∠FEB,
∴∠AEB= ![]() (180°﹣∠DEF),
(180°﹣∠DEF),
∵E为AD边的中点,
∴AE=DE,
∴DE=EF,
∴∠EDF=∠EFD,
∴∠EDF= ![]() (180°﹣∠DEF),
(180°﹣∠DEF),
∴∠AEB=∠EDF,
∴BE∥DG,
∵四边形ABCD是平行四边形,
∴DE∥BG,
∴四边形BEDG为平行四边形;
(2)解:解:如图,∵四边形BEDG为平行四边形,
∴DE=BG,DG=BE=10,
∵四边形ABCD是平行四边形,AE=DE,ABCD的面积等于60,
∴S△ABE= ![]() S平行四边形ABCD=15,
S平行四边形ABCD=15,
连接AF交BE于H,则AH⊥BE,AH=HF,
∵BE=10,
∴AH=3,
∴AF=6,
∵BE∥DG,
∴AF⊥DG,
∴DF= ![]() =8,
=8,
∴FG=DG﹣FD=2.

【解析】(1)根据折的性质得到AE=EF,∠AEB=∠FEB,由平角的定义得到∠AEB= ![]() (180°﹣∠DEF),由三角形的内角和得到∠EDF=
(180°﹣∠DEF),由三角形的内角和得到∠EDF= ![]() (180°﹣∠DEF),根据平行四边形的判定定理即可得到结论;(2)由平行四边形的性质得到DE=BG,DG=BE=10,S△ABE=
(180°﹣∠DEF),根据平行四边形的判定定理即可得到结论;(2)由平行四边形的性质得到DE=BG,DG=BE=10,S△ABE= ![]() S平行四边形ABCD=15,连接AF交BE于H,于是得到AH⊥BE,AH=HF,根据勾股定理即可得到结论.
S平行四边形ABCD=15,连接AF交BE于H,于是得到AH⊥BE,AH=HF,根据勾股定理即可得到结论.
【考点精析】解答此题的关键在于理解平行四边形的判定与性质的相关知识,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D在AC边上,BD=CD,E在BC边上,AE=AB,过点E作EF⊥BC,交AC于F.若AD=5,CE=8,则EF的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】图1、图2是两张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,线段AB、EF的端点均在小正方形的顶点上.
(1)如图1,作出以AB为对角线的正方形并直接写出正方形的周长;
(2)如图2,以线段EF为一边作出等腰△EFG(点G在小正方形顶点处)且顶角为钝角,并使其面积等于4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】道外区劳技学校为了调整重点学科建设和师资配备,对学校开设的四个传统重点学科开展学生较喜爱的学科调查问卷活动(每名学生必选且只选一项).如图是在某中学调查的数据绘制成两幅不完整的统计图,解答下列问题:

(1)求参与本次调查的共有多少名学生?并补全条形统计图.
(2)在扇形统计图中,求喜爱“葫芦烙画”所对应的扇形的圆心角的度数?
(3)若道外区大约有12000名中学生,估计喜欢“陶艺”的共有多少名学生? -
科目: 来源: 题型:
查看答案和解析>>【题目】哈佳高铁建设工程中,有一段6000米的路段由甲、乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成的工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用30天.
(1)求甲、乙两个工程队每天各完成多少米?
(2)由于施工条件限制,每天只能一个工程队施工,但是工程指挥部仍然要求工期不能超过50天,求甲工程队至少施工多少天? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
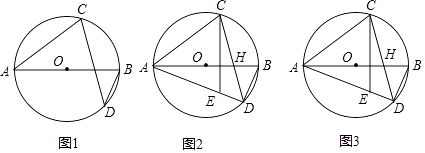
(1)求证:∠ABD=2∠BDC;
(2)过点C作CH⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x(x﹣k)经过原点O,交x轴正半轴于A,过A的直线交抛物线于另一点B,AB交y轴正半轴于C,且OC=OA,B点的纵坐标为9
x(x﹣k)经过原点O,交x轴正半轴于A,过A的直线交抛物线于另一点B,AB交y轴正半轴于C,且OC=OA,B点的纵坐标为9
(1)求抛物线的解析式;
(2)点P为第一象限的抛物线上一点,连接PB、PC,设P点的横坐标为m,△PBC的面积为S,求S与m的函数关系式;
(3)在(2)的条件下,连接OP、AP,若∠APO=45°,求点P的坐标.
相关试题

