【题目】如图,抛物线y= ![]() x(x﹣k)经过原点O,交x轴正半轴于A,过A的直线交抛物线于另一点B,AB交y轴正半轴于C,且OC=OA,B点的纵坐标为9
x(x﹣k)经过原点O,交x轴正半轴于A,过A的直线交抛物线于另一点B,AB交y轴正半轴于C,且OC=OA,B点的纵坐标为9
(1)求抛物线的解析式;
(2)点P为第一象限的抛物线上一点,连接PB、PC,设P点的横坐标为m,△PBC的面积为S,求S与m的函数关系式;
(3)在(2)的条件下,连接OP、AP,若∠APO=45°,求点P的坐标.
参考答案:
【答案】
(1)
解:如图1中,作BH⊥x轴于H.
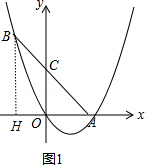
由题意OC=OA=K,∠AOC=90°,
∴∠OAC=∠OCA=45°,
∵∠BHA=90°,
∴∠HBA=∠HAB=45°,
∴BH=AH=9,
∴OH=9﹣k,
∴B(k﹣9,9),
把B(k﹣9,9)代入y= ![]() x(x﹣k),
x(x﹣k),
得到9= ![]() (k﹣9)×(﹣9),
(k﹣9)×(﹣9),
∴k=5,
∴抛物线的解析式为y= ![]() x(x﹣5).
x(x﹣5).
(2)
解:如图2中,作BH⊥x轴于H,连接OP、PH、PA.设P[m, ![]() m(m﹣5)].
m(m﹣5)].
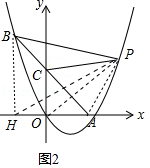
∵P(﹣4,9),A(5,0),C(0,5),
∴S△PBC=S△PAB﹣S△PCA=(S△PBH+S△PHA﹣S△ABH)﹣(S△PCO+S△POA﹣S△AOC)
= ![]() ×9×(m+4)+
×9×(m+4)+ ![]() ×9×
×9× ![]() m(m﹣5)﹣
m(m﹣5)﹣ ![]() ×9×9﹣[
×9×9﹣[ ![]() ×5×m+
×5×m+ ![]() ×5×
×5× ![]() m(m﹣5)﹣
m(m﹣5)﹣ ![]() ×5×5]
×5×5]
= ![]() m2﹣m﹣10(m>5).
m2﹣m﹣10(m>5).
(3)
解:如图3中设AC交OP于D,AC的中点为K,连接PK.
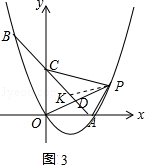
∵∠DPA=∠DCO=45°,∠PDA=CDO,
∴△PDA∽△CDO,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠CDP=∠ODP,
,∵∠CDP=∠ODP,
∴△CDP∽△ODA,
∴∠CPD=∠OAD=45°,
∴∠CPA=90°,
∵CK=KA,
∴PK= ![]() AC=
AC= ![]() ,
,
设P[m, ![]() m(m﹣5)],
m(m﹣5)],
∵K( ![]() ,
, ![]() ),
),
∴(m﹣ ![]() )2+[
)2+[ ![]() m(m﹣5)﹣
m(m﹣5)﹣ ![]() ]2=(
]2=( ![]() )2,
)2,
整理得m(m﹣5)(m2﹣5m﹣4)=0,
∴m=0或5或 ![]() 或
或 ![]() ,
,
∵m>5,
∴m= ![]() ,
,
∴P( ![]() ,1).
,1).
【解析】(1)如图1中,作BH⊥x轴于H.由题意OC=OA=K,∠AOC=90°,推出∠OAC=∠OCA=45°,由∠BHA=90°,推出∠HBA=∠HAB=45°,推出BH=AH=9,推出OH=9﹣k,推出B(k﹣9,9),把B(k﹣9,9)代入y= ![]() x(x﹣k),解方程即可.(2)如图2中,作BH⊥x轴于H,连接OP、PH、PA.设P[m,
x(x﹣k),解方程即可.(2)如图2中,作BH⊥x轴于H,连接OP、PH、PA.设P[m, ![]() m(m﹣5)].根据S△PBC=S△PAB﹣S△PCA=(S△PBH+S△PHA﹣S△ABH)﹣(S△PCO+S△POA﹣S△AOC)计算即可.(3)如图3中设AC交OP于D,AC的中点为K,连接PK.只要证明∠CPA=90°,根据PK=
m(m﹣5)].根据S△PBC=S△PAB﹣S△PCA=(S△PBH+S△PHA﹣S△ABH)﹣(S△PCO+S△POA﹣S△AOC)计算即可.(3)如图3中设AC交OP于D,AC的中点为K,连接PK.只要证明∠CPA=90°,根据PK= ![]() ,利用两点间距离公式,列出方程,解方程即可解决问题.
,利用两点间距离公式,列出方程,解方程即可解决问题.
【考点精析】本题主要考查了等腰直角三角形和函数关系式的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;用来表示函数关系的数学式子叫做函数解析式或函数关系式才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E为AD边的中点,把△ABE沿BE翻折,得到△FBE,连接DF并延长交BC于G.

(1)求证:四边形BEDG为平行四边形.
(2)若BE=AD=10,且ABCD的面积等于60,求FG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】哈佳高铁建设工程中,有一段6000米的路段由甲、乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成的工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用30天.
(1)求甲、乙两个工程队每天各完成多少米?
(2)由于施工条件限制,每天只能一个工程队施工,但是工程指挥部仍然要求工期不能超过50天,求甲工程队至少施工多少天? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
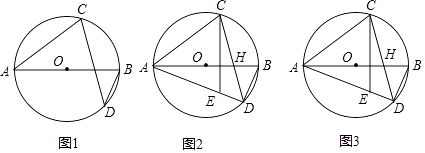
(1)求证:∠ABD=2∠BDC;
(2)过点C作CH⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位运动员在一段2000米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面200米,他们同时同向出发匀速前进,甲的速度是8米/秒,乙的速度是6米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是y米,比赛时间是x秒,当两人都到达终点计时结束,整个过程中y与x之间的函数图象是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式
 的整数解共有4个,则m的取值范围是 .
的整数解共有4个,则m的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AC=
 ,∠A=30°,BC=1,则AB= .
,∠A=30°,BC=1,则AB= .
相关试题

