【题目】在△ABC中,∠ACB=50°,CE为△ABC的角平分线,AC边上的高BD与CE所在的直线交于点F,若∠ABD:∠ACF=3:5,则∠BEC的度数为______.
参考答案:
【答案】100°或130°.
【解析】
分两种情形:①如图1中,当高BD在三角形内部时.②如图2中,当高BD在△ABC外时,分别求解即可.
①如图1中,当高BD在三角形内部时,
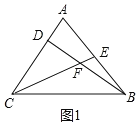
∵CE平分∠ACB,∠ACB=50°,
∴∠ACE=∠ECB=25°.
∵∠ABD:∠ACF=3:5,
∴∠ABD=15°.
∵BD⊥AC,∴∠BDC=90°,
CBD=40°,∴∠CBE=∠CBD+∠ABD=40°+15°=55°,
∴∠BEC=180°﹣∠ECB﹣∠CBE=180°﹣25°﹣55°=100°
②如图2中,当高BD在△ABC外时,
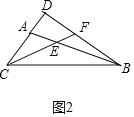
同法可得:∠ABD=25°,∠ABD=15°,∠CBD=40°,
∴∠CBE=∠CBD﹣∠ABD=40°﹣15°=25°,
∴∠BEC=180°﹣25°﹣25°=130°,
综上所述:∠BEC=100°或130°.
故答案为:100°或130°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米。一只小虫在长方体表面从A爬到B的最短路程是__________
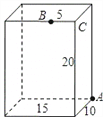
-
科目: 来源: 题型:
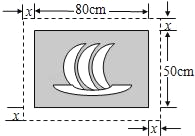
查看答案和解析>>【题目】在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.
(1)求出y关于x的函数解析式,并直接写出自变量的取值范围;
(2)此时金色纸边的宽应为多少cm时,这幅挂图的面积最大?求出最大面积的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:已知二次函数的图象与
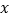 轴交于
轴交于 和
和 两点.交
两点.交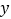 轴于点
轴于点 ,点
,点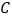 ,
,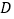 是二次函数图象上的一对对称点,一次函数的图象过点
是二次函数图象上的一对对称点,一次函数的图象过点 ,
,
(1)画出图象,并求二次函数的解析式.
(2)根据图象直接写出使一次函数值大于或等于二次函数值的
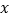 的取值范围.
的取值范围.(3)若直线与
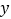 轴交点为
轴交点为 ,连接
,连接 ,
, ,求三角形
,求三角形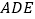 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
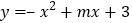 与
与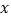 轴的一个交点
轴的一个交点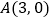 .
.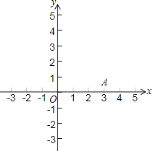
(1)试分别求出这条抛物线与
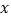 轴的另一个交点
轴的另一个交点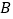 及与
及与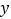 轴的交点
轴的交点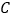 的坐标.
的坐标.(2)设抛物线的顶点为
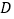 ,请在图中画出抛物线的草图,若点
,请在图中画出抛物线的草图,若点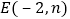 在直线
在直线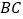 上,试判断
上,试判断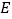 点是否在经过
点是否在经过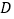 点的反比例函数的图象上,并说明理由;
点的反比例函数的图象上,并说明理由;(3)试求
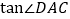 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某星期天,八(1)班开展社会实践活动,第一小组花90元从蔬菜批发市场批发了黄瓜和茄子共40kg,到蔬菜市场去卖,黄瓜和茄子当天的批发价与零售价如表所示:
品名
黄瓜
茄子
批发价/(元/kg)
2.4
2
零售价/(元/kg)
3.6
2.8
(1)黄瓜和茄子各批发了多少kg?
(2)该小组当天卖完这些黄瓜和茄子可赚多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品零售店为食品厂代销一种面包,未售出的面包可以退回厂家.经统计销售情况发现,当这种面包的销售单价为7角时,每天卖出160个.在此基础上.单价每提高1角时,该零售店每天就会少卖出20个面包.设这种面包的销售单价为x角(每个面包的成本是5角).零售店每天销售这种面包的利润为y角.
(1)用含x的代数式分别表示出每个面包的利润与卖出的面包个数;
(2)求x与y之间的函数关系式:
(3)当这种面包的销售单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少元?
相关试题

