【题目】如图,已知抛物线![]() 与
与![]() 轴的一个交点
轴的一个交点![]() .
.
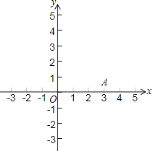
(1)试分别求出这条抛物线与![]() 轴的另一个交点
轴的另一个交点![]() 及与
及与![]() 轴的交点
轴的交点![]() 的坐标.
的坐标.
(2)设抛物线的顶点为![]() ,请在图中画出抛物线的草图,若点
,请在图中画出抛物线的草图,若点![]() 在直线
在直线![]() 上,试判断
上,试判断![]() 点是否在经过
点是否在经过![]() 点的反比例函数的图象上,并说明理由;
点的反比例函数的图象上,并说明理由;
(3)试求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)把A点的坐标代入抛物线的解析式,就可以求出m的值,得到抛物线的解析式.在解析式中令y=0,解方程就可以求出与x轴的交点;(2)根据函数解析式就可求出抛物线的顶点坐标,利用待定系数法求出反比例函数的解析式.经过C,B的直线解析式可以用待定系数法求得,进而求出E点的坐标.把E的坐标代入反比例函数解析式,就可以判断是否在反比例函数的图象上;(3)过D作DF⊥y轴于点F,则△CFD为等腰直角三角形,△AOC是等腰直角三角形,根据勾股定理就可以求出CD,AC的长度.Rt△ADC中根据三角函数的定义就可以求出三角函数值.
解:(1)因为![]() 在抛物线
在抛物线![]() 上,
上,
则![]() ,解得
,解得![]() .
.
所以抛物线的解析式为![]() .
.
因为![]() 点为抛物线与
点为抛物线与![]() 轴的交点,求得
轴的交点,求得![]() ,
,
因为![]() 点为抛物线与
点为抛物线与![]() 轴的交点,求得
轴的交点,求得![]() .
.
(2)∵![]() ,
,
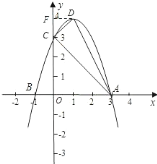
∴顶点![]() ,
,
画这个函数的草图.
由![]() ,
,![]() 点的坐标可求得直线
点的坐标可求得直线![]() 的解析式为
的解析式为![]() ,
,
∵点![]() 在
在![]() 上,
上,
∴![]() .
.
可求得过![]() 点的反比例函数的解析式为
点的反比例函数的解析式为![]() .
.
当![]() 时,
时,![]() .
.
∴点![]() 不在过
不在过![]() 点的反比例函数图象上.
点的反比例函数图象上.
(3)过![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() .
.
连接![]() ,则
,则![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() .
.
因为![]() ,
,
∴![]() 中,
中,![]() .
.
另解:∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
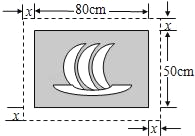
查看答案和解析>>【题目】在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.
(1)求出y关于x的函数解析式,并直接写出自变量的取值范围;
(2)此时金色纸边的宽应为多少cm时,这幅挂图的面积最大?求出最大面积的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:已知二次函数的图象与
 轴交于
轴交于 和
和 两点.交
两点.交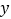 轴于点
轴于点 ,点
,点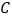 ,
,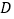 是二次函数图象上的一对对称点,一次函数的图象过点
是二次函数图象上的一对对称点,一次函数的图象过点 ,
,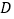
(1)画出图象,并求二次函数的解析式.
(2)根据图象直接写出使一次函数值大于或等于二次函数值的
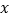 的取值范围.
的取值范围.(3)若直线与
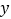 轴交点为
轴交点为 ,连接
,连接 ,
, ,求三角形
,求三角形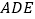 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=50°,CE为△ABC的角平分线,AC边上的高BD与CE所在的直线交于点F,若∠ABD:∠ACF=3:5,则∠BEC的度数为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某星期天,八(1)班开展社会实践活动,第一小组花90元从蔬菜批发市场批发了黄瓜和茄子共40kg,到蔬菜市场去卖,黄瓜和茄子当天的批发价与零售价如表所示:
品名
黄瓜
茄子
批发价/(元/kg)
2.4
2
零售价/(元/kg)
3.6
2.8
(1)黄瓜和茄子各批发了多少kg?
(2)该小组当天卖完这些黄瓜和茄子可赚多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品零售店为食品厂代销一种面包,未售出的面包可以退回厂家.经统计销售情况发现,当这种面包的销售单价为7角时,每天卖出160个.在此基础上.单价每提高1角时,该零售店每天就会少卖出20个面包.设这种面包的销售单价为x角(每个面包的成本是5角).零售店每天销售这种面包的利润为y角.
(1)用含x的代数式分别表示出每个面包的利润与卖出的面包个数;
(2)求x与y之间的函数关系式:
(3)当这种面包的销售单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少元?
-
科目: 来源: 题型:
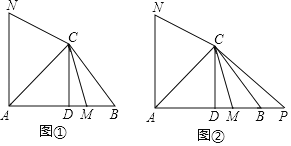
查看答案和解析>>【题目】在△ABC中,∠BAC=45°,CD⊥AB,垂足为点D,M为线段DB上一动点(不包括端点),点N在直线AC左上方且∠NCM=135°,CN=CM,如图①.
(1)求证:∠ACN=∠AMC;
(2)记△ANC得面积为5,记△ABC得面积为5.求证:
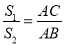 ;
;(3)延长线段AB到点P,使BP=BM,如图②.探究线段AC与线段DB满足什么数量关系时对于满足条件的任意点M,AN=CP始终成立?(写出探究过程)
相关试题

