【题目】阅读下面的例题及点拨,并解决问题:
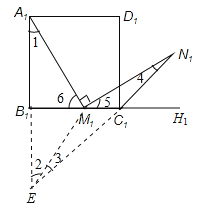
例题:如图①,在等边△ABC中,M是BC边上一点(不含端点B,C),N是△ABC的外角∠ACH的平分线上一点,且AM=MN.求证:∠AMN=60°.
点拨:如图②,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM.易证:△ABM≌△EBM(SAS),可得AM=EM,∠1=∠2;又AM=MN,则EM=MN,可得∠3=∠4;由∠3+∠1=∠4+∠5=60°,进一步可得∠1=∠2=∠5,又因为∠2+∠6=120°,所以∠5+∠6=120°,即:∠AMN=60°.
问题:如图③,在正方形A1B1C1D1中,M1是B1C1边上一点(不含端点B1,C1),N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,且A1M1=M1N1.求证:∠A1M1N1=90°.

参考答案:
【答案】见解析;
【解析】
延长A1B1至E,使EB1=A1B1,连接EM1C、EC1,则EB1=B1C1,∠EB1M1=90°=∠A1B1M1,得出△EB1C1是等腰直角三角形,由等腰直角三角形的性质得出∠B1EC1=∠B1C1E=45°,证出∠B1C1E+∠M1C1N1=180°,得出E、C1、N1,三点共线,由SAS证明△A1B1M1≌△EB1M1得出A1M1=EM1,∠1=∠2,得出EM1=M1N1,由等腰三角形的性质得出∠3=∠4,证出∠1=∠2=∠5,得出∠5+∠6=90°,即可得出结论.
解:延长A1B1至E,使EB1=A1B1,连接EM1、EC1,
如图所示:
则EB1=B1C1,∠EB1M1=90°=∠A1B1M1,
∴△EB1C1是等腰直角三角形,
∴∠B1EC1=∠B1C1E=45°,
∵N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,
∴∠M1C1N1=90°+45°=135°,
∴∠B1C1E+∠M1C1N1=180°,
∴E、C1、N1三点共线,
在△A1B1M1和△EB1M1中, ,
,
∴△A1B1M1≌△EB1M1(SAS),
∴A1M1=EM1,∠1=∠2,
∵A1M1=M1N1,
∴EM1=M1N1,
∴∠3=∠4,
∵∠2+∠3=45°,∠4+∠5=45°,
∴∠1=∠2=∠5,
∵∠1+∠6=90°,
∴∠5+∠6=90°,
∴∠A1M1N1=180°﹣90°=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).

(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求S△COB . -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x
…
-3
-2
-1
0
1
2
3
4
5
…
y
…
12
5
0
-3
-4
-3
0
5
12
…
下列四个结论:
①二次函数y=ax2+bx+c 有最小值,最小值为-3;
②抛物线与y轴交点为(0,-3);
③二次函数y=ax2+bx+c 的图像对称轴是x=1;
④本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
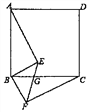
查看答案和解析>>【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某区九年级学生课外体育活动的情况,从该年级学生中随机抽取了4%的学生,对其参加的体育活动项目进行了调查,将调查的数据进行统计并绘制成如图所示的扇形统计图和条形统计图.有下列结论:①被抽测学生中参加羽毛球项目的人数为30;②在本次调查中“其他”的扇形的圆心角的度数为36°;③估计全区九年级参加篮球项目的学生比参加足球项目的学生多20%;④全区九年级大约有1500名学生参加乒乓球项目.其中正确结论的个数是( )

A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】图中折线表示芳芳骑自行车离家的距离与时间的关系,她9点离开家,15点回家,请根据图象回答下列问题:

(1)芳芳到达离家最远的地方时,离家________千米;
(2)第一次休息时离家________ 千米;
(3)她在10:00~10:30的平均速度是_________;
(4)芳芳一共休息了_________ 小时;
(5)芳芳返回用了____________小时;
(6)返回时的平均速度是__________.
-
科目: 来源: 题型:
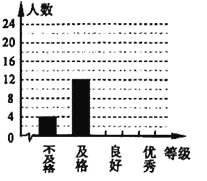
查看答案和解析>>【题目】某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制成图表时发现,优秀漏统计
 人,良好漏统计
人,良好漏统计 人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生
 人,请你估算出该校体能测试等级为“优秀”的人数.
人,请你估算出该校体能测试等级为“优秀”的人数.学生体能测试成绩各等次人数统计表
体能等级
调整前人数
调整后人数
优秀

良好

及格

不及格

合计

学生体能测试成绩各等次人数统计图
相关试题

