搜索
【题目】图中折线表示芳芳骑自行车离家的距离与时间的关系，她9点离开家，15点回家，请根据图象回答下列问题：
（1）芳芳到达离家最远的地方时，离家________千米；
（2）第一次休息时离家________ 千米；
（3）她在10：00~10：30的平均速度是_________；
（4）芳芳一共休息了_________ 小时；
（5）芳芳返回用了____________小时；
（6）返回时的平均速度是__________．
参考答案：
【答案】（1）30，（2）17，（3）14km/h，（4）1.5，（5）2，（6）15km/h．
【解析】
（1）E点的纵坐标是30，
∴到达最远地方离家30千米．
（2）C点开始第一次休息，纵坐标是17，
∴第一次休息时离家17千米．
（3）（17-10）÷0.5=14km/h．
（4）（11-10.5）+（13-12）=1.5（小时）．
（5）15-13=2小时．
（6）30÷2=15km/h．
-
科目： 来源： 题型：
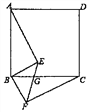
查看答案和解析>>【题目】如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G.
(1)求证：AE=CF；
(2)若∠ABE=55°，求∠EGC的大小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面的例题及点拨，并解决问题：
例题：如图①，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC的外角∠ACH的平分线上一点，且AM=MN．求证：∠AMN=60°．
点拨：如图②，作∠CBE=60°，BE与NC的延长线相交于点E，得等边△BEC，连接EM．易证：△ABM≌△EBM（SAS），可得AM=EM，∠1=∠2；又AM=MN，则EM=MN，可得∠3=∠4；由∠3+∠1=∠4+∠5=60°，进一步可得∠1=∠2=∠5，又因为∠2+∠6=120°，所以∠5+∠6=120°，即：∠AMN=60°．
问题：如图③，在正方形A1B1C1D1中，M1是B1C1边上一点（不含端点B1，C1），N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，且A1M1=M1N1．求证：∠A1M1N1=90°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解某区九年级学生课外体育活动的情况，从该年级学生中随机抽取了4%的学生，对其参加的体育活动项目进行了调查，将调查的数据进行统计并绘制成如图所示的扇形统计图和条形统计图.有下列结论：①被抽测学生中参加羽毛球项目的人数为30；②在本次调查中“其他”的扇形的圆心角的度数为36°；③估计全区九年级参加篮球项目的学生比参加足球项目的学生多20%；④全区九年级大约有1500名学生参加乒乓球项目.其中正确结论的个数是（ ）
A. 1B. 2C. 3D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校为了解学生体质情况，从各年级随机抽取部分学生进行体能测试，每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制成图表时发现，优秀漏统计
人，良好漏统计
人，于是及时更正,从而形成如下图表.请按正确数据解答下列各题：(1)填写统计表．
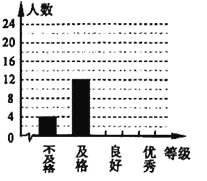
(2)根据调整后数据，补全条形统计图．
(3)若该校共有学生
人，请你估算出该校体能测试等级为“优秀”的人数．学生体能测试成绩各等次人数统计表
体能等级
调整前人数
调整后人数
优秀
良好
及格
不及格
合计
学生体能测试成绩各等次人数统计图
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了贯彻落实中央提出的“厉行节约，反对浪费”的精神，某校学生自发组织了“保护水源，从我做起”的活动，学生们对我国“水资源问题”进行了调查，发现我国水资源越来越匮乏，可是人们的节约意识并不强.据查，仅某饮料厂每天从地下抽水达3500立方米左右.同学们采取问卷调查的方式，随机调查了本校150名同学家庭人均月用水量和节水措施情况.以下是根据调查结果作出的部分统计图：
请根据以上信息，解答以下问题：
（1）补全图①和图②；
（2）为提高人们的节水意识，请你写出一条与图②中已明确的节水措施不同的节水措施.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC是直角三角形，延长AB到点E，使BE=BC，在BC上取一点F，使BF=AB，连接EF．△ABC旋转后能与△FBE重合，请回答：
（1）旋转中心是点 ，
（2）旋转了度，
（3）AC与EF的关系为.
相关试题
