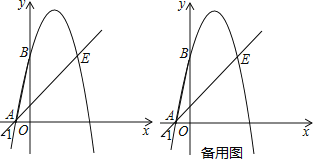
【题目】如图,抛物线y=ax2+4x+c(a≠0)经过点A(﹣1,0),点E(4,5),与y轴交于点B,连接AB.
(1)求该抛物线的解析式;
(2)将△ABO绕点O旋转,点B的对应点为点F.
①当点F落在直线AE上时,求点F的坐标和△ABF的面积;
②当点F到直线AE的距离为![]() 时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标.
时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标.
参考答案:
【答案】(1)抛物线的解析式是y=﹣x2+4x+5;(2)①当F(﹣4,﹣3)时,S△ABF=6;当F(3,4)时,S△ABF=8;②F点的坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
【解析】(1)将点A、E的坐标代入利用待定系数法进行求解即可得;
(2)①先利用待定系数法求得直线AE的解析式,然后利用旋转的性质求得点F坐标,分情况进行讨论即可得;
②由题意可知直线AE向上平移2个单位或向下平移2个单位,求出平移后的解析式然后分别与二次函数的解析式联立组成方程组进行求解即可得.
(1)将A,E点坐标代入函数解析式,得
![]() ,解得
,解得![]() ,
,
抛物线的解析式是y=﹣x2+4x+5;
(2)①设AE的解析式为y=kx+b,将A,E点坐标代入,得
![]() ,解得
,解得![]() ,
,
AE的解析式为y=x+1,x=0时,y=1,即C(0,1),
设F点坐标为(n,n+1),由旋转的性质得:OF=OB=5,n2+(n+1)2=25,
解得n1=﹣4,n2=3,F(﹣4,﹣3),F(3,4),
当F(﹣4,﹣3)时,如图1,
 ,
,
S△ABF=S△BCF﹣S△ABC=![]() BC|xF|﹣
BC|xF|﹣![]() BC|xA|=
BC|xA|=![]() BC(xA﹣xF),
BC(xA﹣xF),
S△ABF=![]() ×4(﹣1+4)=6;
×4(﹣1+4)=6;
当F(3,4)时,如图2,
 ,
,
S△ABF=S△BCF+S△ABC=![]() BC|xF|+
BC|xF|+![]() BC|xA|=
BC|xA|=![]() BC(xF﹣xA),
BC(xF﹣xA),
S△ABF=![]() ×4(3+1)=8;
×4(3+1)=8;
②如图3,

∵∠HCG=∠ACO,∠HGC=∠COA,∴△HGC∽△COA,
∵OA=OC=1,∴CG=HG=![]() ,由勾股定理,得HC=
,由勾股定理,得HC=![]() =2,
=2,
直线AE向上平移2个单位或向下平移2个单位,
l的解析是为y=x+3,l1的解析是为y=x﹣1,
联立![]() ,
,
解得 ,
, ,
,
![]() ,解得
,解得 ,
, ,
,
F点的坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
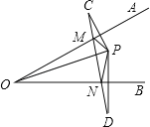
查看答案和解析>>【题目】如图,∠AOB=30°,P是∠AOB内的一点,且OP=4cm,C、D分别是P关于OA、OB的对称点,连结CD、PM、PN,则△PMN的周长为________.
-
科目: 来源: 题型:
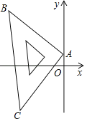
查看答案和解析>>【题目】把一个等腰直角三角板放在黑板上画好了的平面直角坐标系内,如图,已知直角顶点A的坐标为(0,1),另一个顶点B的坐标为(﹣5,5),则点C的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 、
、 在数轴上,
在数轴上,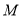 对应的数是
对应的数是 ,点
,点 在
在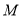 的右边,且距
的右边,且距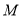 点4个单位长度,点
点4个单位长度,点 、
、 是数轴上两个动点;
是数轴上两个动点;(1)点
 所对应的数为 ;
所对应的数为 ;(2)当点
 到点
到点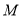 、
、 的距离之和是5个单位时,点
的距离之和是5个单位时,点 所对应的数是多少?
所对应的数是多少?(3)如果
 、
、 分别从点
分别从点 、
、 出发,均沿数轴向左运动,点
出发,均沿数轴向左运动,点 每秒走2个单位长度,先出发5秒钟,点
每秒走2个单位长度,先出发5秒钟,点 每秒走3个单位长度,当
每秒走3个单位长度,当 、
、 两点相距2个单位长度时,点
两点相距2个单位长度时,点 、
、 对应的数各是多少?
对应的数各是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长,b在数轴上表示的点在原点右侧,距离原点2个单位长,c和d互为倒数,m与n互为相反数,y为最大的负整数,求(y+b)2+m(a-cd)-nb2的值.
-
科目: 来源: 题型:
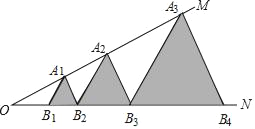
查看答案和解析>>【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1B2、△A2B2B3、△A3B3B4、…均为等边三角形,若OB1=1,则△A8B8B9的边长为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(﹣1,2),B(﹣4,1),C(﹣2,﹣2)
(1)请写出△ABC关于x轴对称的点A1、B1、C1的坐标;
(2)请在这个坐标系中作出△ABC关于y轴对称的△A2B2C2;
(3)计算:△A2B2C2的面积.

相关试题

