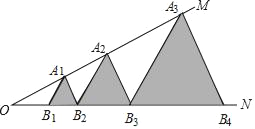
【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1B2、△A2B2B3、△A3B3B4、…均为等边三角形,若OB1=1,则△A8B8B9的边长为_____
参考答案:
【答案】128
【解析】
由等边三角形的性质可证得B2A1⊥OA1,再根据30°角所对的直角边是斜边的一半可求得B2A1= ![]() OB2,依此类推可求得答案.
OB2,依此类推可求得答案.
∵△B1A1B2为等边三角形,
∴∠A1B1B2=60°,
∵∠MON=30°,
∴∠OA1B2=30°+60°=90°,
∴B2A1=![]() OB2,
OB2,
同理可求得:A4B5=![]() OB5,
OB5,
∵OB1=1,
∴OB4=2OB3=4OB2=8OB1=8,OB5=2OB4=4OB3=8OB2=16OB1=16,
∴B4B5=OB5OB4=168=8,
以此类推: B8B9=128
故答案为128.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
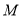 、
、 在数轴上,
在数轴上,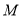 对应的数是
对应的数是 ,点
,点 在
在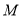 的右边,且距
的右边,且距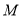 点4个单位长度,点
点4个单位长度,点 、
、 是数轴上两个动点;
是数轴上两个动点;(1)点
 所对应的数为 ;
所对应的数为 ;(2)当点
 到点
到点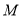 、
、 的距离之和是5个单位时,点
的距离之和是5个单位时,点 所对应的数是多少?
所对应的数是多少?(3)如果
 、
、 分别从点
分别从点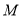 、
、 出发,均沿数轴向左运动,点
出发,均沿数轴向左运动,点 每秒走2个单位长度,先出发5秒钟,点
每秒走2个单位长度,先出发5秒钟,点 每秒走3个单位长度,当
每秒走3个单位长度,当 、
、 两点相距2个单位长度时,点
两点相距2个单位长度时,点 、
、 对应的数各是多少?
对应的数各是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+4x+c(a≠0)经过点A(﹣1,0),点E(4,5),与y轴交于点B,连接AB.
(1)求该抛物线的解析式;
(2)将△ABO绕点O旋转,点B的对应点为点F.
①当点F落在直线AE上时,求点F的坐标和△ABF的面积;
②当点F到直线AE的距离为
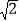 时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标.
时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标.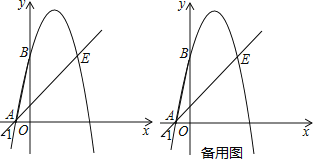
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长,b在数轴上表示的点在原点右侧,距离原点2个单位长,c和d互为倒数,m与n互为相反数,y为最大的负整数,求(y+b)2+m(a-cd)-nb2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(﹣1,2),B(﹣4,1),C(﹣2,﹣2)
(1)请写出△ABC关于x轴对称的点A1、B1、C1的坐标;
(2)请在这个坐标系中作出△ABC关于y轴对称的△A2B2C2;
(3)计算:△A2B2C2的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的解题过程,再解决问题.
解方程: x4 -6x2 +5=0.
这是一个一元四次方程,根据该方程的特点,它的通常解法是:
设 x2 = y ,则原方程可化为 y2 -6y+5=0.①
解这个方程,得 y1 =1, y2 =5.当 y =1时, x=±1;当 y=5时, x=±
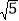 .所以原方程有四个根: x1 =1, x2 =-1, x3 =
.所以原方程有四个根: x1 =1, x2 =-1, x3 =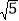 , x4 =-
, x4 =-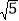 .
. (1)填空:在由原方程得到方程①的过程中,利用________法达到降次的目的,体现了________的数学思想.
(2)解方程:( x2 -x )2 -4(x2 -x )-12=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,∠ABC=35°,E是BC边上一点且AE=CE,D是
BC边上的中点,连接AD,AE.
(1)求∠DAE的度数;
(2)若BD上存在点F,且∠AFE=∠AEF,求证:BF=CE.

相关试题

