【题目】如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程. 证明:∵BE平分∠ABC,∴∠1=∠3. ()
又∵∠1=∠2(已知),∴=( 等量代换),
∴∥()
∴∠AED=∠C ().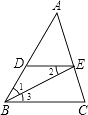
参考答案:
【答案】已知;∠2;∠3;DE;BC;内错角相等,两直线平行;两直线平行,同位角相等
【解析】证明:∵BE平分∠ABC, ∴∠1=∠3(角平分线定义),
又∵∠1=∠2(已知),
∴∠2=∠3(等量代换),
∴DE∥BC(内错角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
故答案为:已知,∠2,∠3,DE,BC,内错角相等,两直线平行,两直线平行,同位角相等.
先根据等量代换,得出∠2=∠3,再根据平行线的判定,得出DE∥BC,最后根据平行线的性质,得出∠AED=∠C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究证明:
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数列3、12、30、60……中,请你观察数列的排列规律,则第5个数是( )
A. 75B. 90C. 105D. 120
-
科目: 来源: 题型:
查看答案和解析>>【题目】试验与探究:我们知道分数写
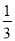 为小数即
为小数即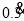 ,反之,无限循环小数
,反之,无限循环小数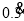 写成分数即
写成分数即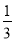 .一般地,任何一个无限循环小数都可以写成分数形式.现在就以
.一般地,任何一个无限循环小数都可以写成分数形式.现在就以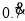 为例进行讨论:设
为例进行讨论:设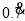 =x,由
=x,由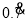 =0.7777…,可知,10x-x=7.77…-0.777…=7,即10x-x=7,解方程得
=0.7777…,可知,10x-x=7.77…-0.777…=7,即10x-x=7,解方程得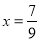 ,于是得
,于是得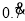 =
=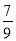
请仿照上述例题完成下列各题:
(1)请你把无限循环小数
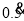 写成分数,即
写成分数,即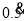 =__________
=__________(2)你能化无限循环小数
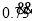 为分数吗?请仿照上述例子求解之.
为分数吗?请仿照上述例子求解之. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个实数中,比﹣1小的数是( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数﹣3,2,0,﹣1中,最大的实数是( )
A. ﹣3B. 2C. 0D. ﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数的图象经过点(-1,0),且函数值随自变量的增大而减小,符合要求的函数的解析式可以是:(写出一个即可)___________ .
相关试题

