【题目】探究证明:
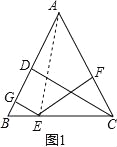
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
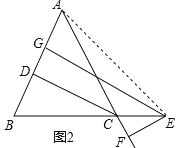
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
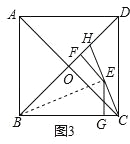
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .

参考答案:
【答案】(1)证明见解析
(2)CD=EG﹣EF,
(3)5![]() .
.
【解析】
试题分析:(1)根据S△ABC=S△ABE+S△ACE,得到![]() ABCD=
ABCD=![]() ABEG+
ABEG+![]() ACEF,根据等式的性质即可得到结论;
ACEF,根据等式的性质即可得到结论;
(2)由于S△ABC=S△ABE﹣S△ACE,于是得到![]() ABCD=
ABCD=![]() ABEG﹣
ABEG﹣![]() ACEF,根据等式的性质即可得到结论;
ACEF,根据等式的性质即可得到结论;
(3)根据正方形的性质得到AB=BC=10,∠ABC=90°,AC⊥BD,根据勾股定理得到AC=10![]() ,由于S△BCH=S△BCE+S△BHE,得到
,由于S△BCH=S△BCE+S△BHE,得到![]() BHOC=
BHOC=![]() BCEG+
BCEG+![]() BHEF,根据等式的性质即可得到结论.
BHEF,根据等式的性质即可得到结论.
试题解析:(1)如图1,连接AE,
∵EG⊥AB,EF⊥AC,CD⊥AB,
∵S△ABC=S△ABE+S△ACE,
∴![]() ABCD=
ABCD=![]() ABEG+
ABEG+![]() ACEF,
ACEF,
∵AB=AC,
∴CD=EG+EF;
(2)CD=EG﹣EF,
理由:连接AE,
∵EG⊥AB,EF⊥AC,CD⊥AB,
∵S△ABC=S△ABE﹣S△ACE,
∴![]() ABCD=
ABCD=![]() ABEG﹣
ABEG﹣![]() ACEF,
ACEF,
∵AB=AC,
∴CD=EG﹣EF;
故答案为:CD=EG﹣EF;
(3)∵四边形ABCD是正方形,
∴AB=BC=10,∠ABC=90°,AC⊥BD,
∴AC=10![]() ,
,
∴OC=![]() AC=5
AC=5![]() ,
,
连接BE.
∵EF⊥BD于点F,EG⊥BC于点G,
∵S△BCH=S△BCE+S△BHE,
∴![]() BHOC=
BHOC=![]() BCEG+
BCEG+![]() BHEF,
BHEF,
∴OC=EG+EF=5![]() ,
,
故答案为:5![]() .
.



-
科目: 来源: 题型:
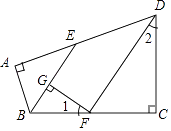
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】3与﹣4的大小关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE是位于公路边的电线杆,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根水泥撑杆BD,用于撑起拉线.已知公路的宽AB为8米,电线杆AE的高为12米,水泥撑杆BD高为6米,拉线CD与水平线AC的夹角为67.4°.求拉线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计).(参考数据:sin67.4°≈
 ,cos67.4°≈
,cos67.4°≈ ,tan67.4°≈
,tan67.4°≈ )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数列3、12、30、60……中,请你观察数列的排列规律,则第5个数是( )
A. 75B. 90C. 105D. 120
-
科目: 来源: 题型:
查看答案和解析>>【题目】试验与探究:我们知道分数写
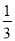 为小数即
为小数即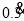 ,反之,无限循环小数
,反之,无限循环小数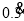 写成分数即
写成分数即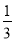 .一般地,任何一个无限循环小数都可以写成分数形式.现在就以
.一般地,任何一个无限循环小数都可以写成分数形式.现在就以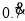 为例进行讨论:设
为例进行讨论:设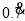 =x,由
=x,由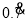 =0.7777…,可知,10x-x=7.77…-0.777…=7,即10x-x=7,解方程得
=0.7777…,可知,10x-x=7.77…-0.777…=7,即10x-x=7,解方程得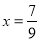 ,于是得
,于是得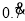 =
=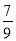
请仿照上述例题完成下列各题:
(1)请你把无限循环小数
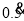 写成分数,即
写成分数,即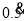 =__________
=__________(2)你能化无限循环小数
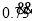 为分数吗?请仿照上述例子求解之.
为分数吗?请仿照上述例子求解之. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程. 证明:∵BE平分∠ABC,∴∠1=∠3. ()
又∵∠1=∠2(已知),∴=( 等量代换),
∴∥()
∴∠AED=∠C ().
相关试题

