【题目】定义:至少有一组对边相等的四边形为“等对边四边形”.

(1)请写出一个你学过的特殊四边形中是“等对边四边形”的名称;
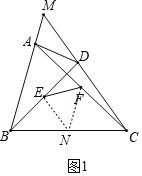
(2)如图1,四边形ABCD是“等对边四边形”,其中AB=CD,边BA与CD的延长线交于点M,点E、F是对角线AC、BD的中点,若∠M=60°,求证:EF![]() AB;
AB;
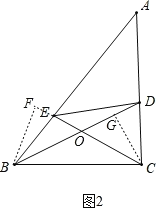
(3)如图2.在△ABC中,点D、E分别在边AC、AB上,且满足∠DBC=∠ECB![]() ∠A,线段CE、BD交于点.
∠A,线段CE、BD交于点.
①求证:∠BDC=∠AEC;
②请在图中找到一个“等对边四边形”,并给出证明.
参考答案:
【答案】(1)如:平行四边形、矩形、菱形、等腰梯形等;(2)证明见解析;(3)①证明见解析;②四边形EBCD是等对边四边形.证明见解析.
【解析】
(1)理解等对边四边形的图形的定义,有平行四边形、矩形、菱形、等腰梯形等,可得出答案.
(2)取BC的中点N,连结EN,FN,由中位线定理可得EN=12CD,FN=12AB,可证明△EFN为等边三角形,则结论得证;
(3)①证明∠EOB=∠A,利用四边形内角和可证明∠BDC=∠AEC;
②作CG⊥BD于G点,作BF⊥CE交CE延长线于F点.根据AAS可证明△BCF≌△CBG,则BF=CG,证明△BEF≌△CDG,可得BE=CD,则四边形EBCD是“等对边四边形”.
(1)如:平行四边形、矩形、菱形、等腰梯形等.
(2)如图1,取BC的中点N,连结EN,FN,
∴EN![]() CD,FN
CD,FN![]() AB,
AB,
∴EN=FN.
∵∠M=60°,
∴∠MBC+∠MCB=120°.
∵FN∥AB,EN∥MC,
∴∠FNC=∠MBC,∠ENB=∠MCB,
∴∠ENF=180°﹣120°=60°,
∴△EFN为等边三角形,
∴EF=FN![]() AB.
AB.
(3)①证明:∵∠BOE=∠BCE+∠DBC,∠DBC=∠ECB![]() ∠A,
∠A,
∴∠BOE=2∠DBC=∠A.
∵∠A+∠AEC+∠ADB+∠EOD=360°,∠BOE+∠EOD=180°,
∴∠AEC+∠ADB=180°.
∵∠ADB+∠BDC=180°,
∴∠BDC=∠AEC;
②解:此时存在等对边四边形,是四边形EBCD.
如图2,作CG⊥BD于G点,作BF⊥CE交CE延长线于F点.
∵∠DBC=∠ECB![]() ∠A,BC=CB,∠BFC=∠BGC=90°,
∠A,BC=CB,∠BFC=∠BGC=90°,
∴△BCF≌△CBG(AAS),
∴BF=CG.
∵∠BEF=∠ABD+∠DBC+∠ECB,∠BDC=∠ABD+∠A,
∴∠BEF=∠BDC,
∴△BEF≌△CDG(AAS),
∴BE=CD,
∴四边形EBCD是等对边四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,C(0,a),D(b,a),其中a,b满足关系式:|a+3|+(b-a+1)2=0.
(1)a=___,b=___,△BCD的面积为______;
(2)如图2,若AC⊥BC,点P线段OC上一点,连接BP,延长BP交AC于点Q,当∠CPQ=∠CQP时,求证:BP平分∠ABC;
(3)如图3,若AC⊥BC,点E是点A与点B之间一动点,连接CE,CB始终平分∠ECF,当点E在点A与点B之间运动时,
 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD,把△BCD沿BD翻折,得△BDG,BG,AD所在的直线交于点E,过点D作DF∥BE交BC所在直线于点F.

(1)求证:四边形DEBF是菱形;
(2)若AB=8,AD=4,求四边形BEDF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为( )

A.120°B.135°C.150°D.不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点 E 在正方形 ABCD 的 AB 边上(不与点 A,B 重合),BD 是对角线,延长 AB 到点 F,使 BF=AE,过点 E 作 BD 的垂线,垂足为 M,连接 AM,CF.
(1)求证:MB=ME;
(2)①用等式表示线段 AM 与 CF 的数量关系,并证明;
②用等式表示线段 AM,BM,DM 之间的数量关系,并说明理由.

-
科目: 来源: 题型:
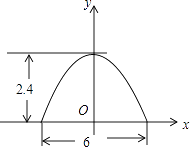
查看答案和解析>>【题目】某菜农搭建了一个横截面为抛物线的大棚,尺寸如图,若菜农身高为1.8m,他在不弯腰的情况下,在棚内的横向活动范围是m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为 40m 的栅栏围住(如图).设绿化带的BC 边长为x m,绿化带的面积为y m2 .
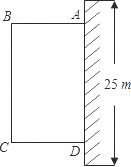
(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围.
(2)当x 为何值时,满足条件的绿化带的面积最大?
相关试题

