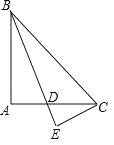
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为( )

A.120°B.135°C.150°D.不能确定
参考答案:
【答案】B
【解析】
先根据∠1+∠2=90°得出∠EAM+∠EDN的度数,再由角平分线的定义得出∠EAF+∠EDF的度数,根据AE⊥DE可得出∠3+∠4的度数,进而可得出∠FAD+∠FDA的度数,由三角形内角和定理即可得出结论.
解:

∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°-90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=![]() ×270°=135°.
×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°-90°=45°,
∴∠F=180°-(∠FAD+∠FDA)=180-45°=135°.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)
 (x﹣5)=3﹣
(x﹣5)=3﹣ (x﹣5)
(x﹣5)(3)
 ﹣1=
﹣1=
(4)x﹣
 (x﹣9)=
(x﹣9)= [x+
[x+ (x﹣9)]
(x﹣9)](5)
 -
- =0.5x+2
=0.5x+2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E,若BD=10,则CE=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:

(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)求△ABC的面积为_______;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线 AB、CD 相交于 O,∠BOC=70°,OE 是∠BOC 的角平分线,OF是OE的反向延长线.
(1)求∠1,∠2,∠3 的度数;
(2)判断 OF 是否平分∠AOD,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系中,已知
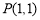 ,过点
,过点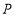 分别向
分别向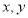 轴作垂线,垂足分别是
轴作垂线,垂足分别是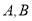 ;
;(1)点Q在直线
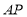 上且与点P的距离为2,则点Q的坐标为__________
上且与点P的距离为2,则点Q的坐标为__________(2)平移三角形
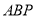 ,若顶点P平移后的对应点
,若顶点P平移后的对应点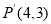 ,画出平移后的三角形
,画出平移后的三角形 .
.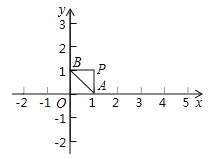
相关试题

