【题目】在直角坐标系xOy中，ABCD四个顶点的坐标分别为A（1，1），B（4，1），C（5，2），D（2，2），直线l：y=kx+b与直线y=﹣2x平行．

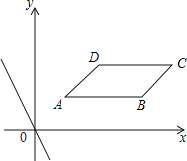
（1）k= ；

（2）若直线l过点D，求直线l的解析式；

（3）若直线l同时与边AB和CD都相交，求b的取值范围；

（4）若直线l沿线段AC从点A平移至点C，设直线l与x轴的交点为P，问是否存在一点P，使△PAB为等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．

参考答案：

【答案】（1）-2；（2）y=﹣2x+6；（3）3≤b≤12；（4）（，0）或（2+1，0）或（4﹣2，0）

【解析】

试题分析：（1）根据平行的条件，一次项系数相同，据此即可求得；

（2）设直线l的解析式是y=﹣2x+b，把D的坐标代入解析式即可求得b的值，即可得到函数的解析式；

（3）求得经过A和C的解析式，即可求得；

（4）分成PA=PB和AP=AB和BP=BA三种情况进行讨论即可求解．

解：（1）k=﹣2；

（2）设直线l的解析式是y=﹣2x+b，

把（2，2）代入得：﹣4+b=2，解得：b=6，

则直线l的解析式是y=﹣2x+6；

（3）设过A直线l的解析式是y=﹣2x+b，把（1，1）代入得：﹣2+c=1，解得：c=3，

则直线的解析式是y=﹣2x+3，

同理，过C直线l的解析式是y=﹣2x+12，

则3≤b≤12；

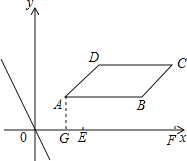
（4）当直线l经过A时，解析式是y=﹣2x+3，令y=0，解得x=，即与x轴的交点是E（，0）；

当直线l经过C时，解析式是y=﹣2x+12，令y=0，解得x=6，即与x轴的交点是F（6，0）；

当PA=PB时，P在AB的中垂线上，则P的坐标是（，0）；

当AP=AB=3时，则PG==2，则P的坐标是（2+1，0）；

同理，当BP=BA=3时，P的坐标是（4﹣2，0）．

故P的坐标是：（，0）或（2+1，0）或（4﹣2，0）．

关闭