【题目】如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=![]() (k≠0)上,则k的值为( )
(k≠0)上,则k的值为( )

A.4 B.﹣2 C.![]() D.﹣
D.﹣![]()
参考答案:
【答案】D
【解析】
试题分析:设点C的坐标为(x,y),过点C作CD⊥x轴,作CE⊥y轴,由折叠的性质易得∠CAB=∠OAB=30°,AC=AO=2,∠ACB=AOB=90°,用锐角三角函数的定义得CD,CE,得点C的坐标,易得k.
解:设点C的坐标为(x,y),过点C作CD⊥x轴,作CE⊥y轴,
∵将△ABO沿直线AB翻折,
∴∠CAB=∠OAB=30°,AC=AO=2,∠ACB=AOB=90°,
∴CD=y=ACsin60°=2×![]() =
=![]() ,
,
∵∠ACB=∠DCE=90°,
∴∠BCE=∠ACD=30°,
∵BC=BO=AOtan30°=2×![]() =
=![]() ,
,
CE=x=BCcos30°=![]() =1,
=1,
∵点C恰好落在双曲线y=![]() (k≠0)上,
(k≠0)上,
∴k=xy=﹣1×![]() =﹣
=﹣![]() ,
,
故选D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】和点P(-3,2)关于y轴对称的点是( )
A.(3, 2) B.(-3,2) C. (3,-2) D.(-3,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知A(2,-2),在y轴上确定点P,使△AOP为等腰三角形,则符合条件的点有 ( )
A.2个 B.3个 C.4个 D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=﹣2x平行.
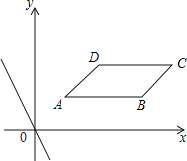
(1)k= ;
(2)若直线l过点D,求直线l的解析式;
(3)若直线l同时与边AB和CD都相交,求b的取值范围;
(4)若直线l沿线段AC从点A平移至点C,设直线l与x轴的交点为P,问是否存在一点P,使△PAB为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是外角和的2倍,则这个多边形是( )
A. 四边形 B. 五边形 C. 六边形 D. 八边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)4a2﹣16 ; (2)(x+2)(x+4)+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
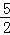 ,y2)是抛物线上两点,则y1<y2,其中说法正确的是( )
,y2)是抛物线上两点,则y1<y2,其中说法正确的是( )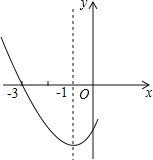
A.①② B.②③ C.①②④ D.②③④
相关试题

