【题目】某班级为准备元旦联欢会,欲购买价格分别为2元、4元和10元的三种奖品,每种奖品至少购买一件,共买16件,恰好用50元.若2元的奖品购买a件.
(1)用含a的代数式表示另外两种奖品的件数;
(2)请你设计购买方案,并说明理由.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)第一种:三种奖品分别购买10、5、1件;(2元的10件,4元的5件,10元的1件.)第二种:三种奖品分别购买13、1、2件.(2元的13件,4元的1件,10元的2件).
;(2)第一种:三种奖品分别购买10、5、1件;(2元的10件,4元的5件,10元的1件.)第二种:三种奖品分别购买13、1、2件.(2元的13件,4元的1件,10元的2件).
【解析】
试题(1)应设出另外两种奖品的件数,根据件数和钱数来解答;
(2)根据取值范围及整数值来确定购买方案.
试题解析:(1)设三种奖品各a,b,c件,则a≥1,b≥1,c≥1,
![]() ,解方程组得:
,解方程组得:![]() .
.![]() .
.
(2)因为b≥1,![]() ,所以
,所以![]() ,解得:
,解得:![]() ,
,
因为c≥1,![]() ,所以
,所以![]() ,解得:
,解得:![]() ,
,
解得,![]() ,
,
当a=10时,b和c有整数解,则a=10,b=5,c=1;
当a=13时,b和c有整数解,则a=13,b=1,c=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 与
与 轴交于
轴交于 ,
,  ,与
,与 轴交于
轴交于 .
. (1)若
 ,求抛物线的解析式,并写出抛物线的对称轴;
,求抛物线的解析式,并写出抛物线的对称轴;(2)如图1,在(1)的条件下,设抛物线的对称轴交轴于
 ,在对称轴左侧的抛物线上有一点
,在对称轴左侧的抛物线上有一点 ,使
,使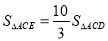 ,求点
,求点 的坐标;
的坐标;(3)如图2,设
 ,
,  于
于 ,在线段
,在线段 上是否存在点
上是否存在点 ,使
,使 ?若存在,求
?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.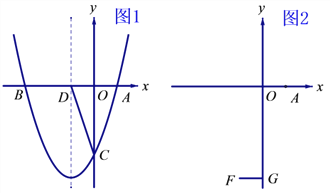
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一组对边相等目这一组对边所在直线互相垂直的凸四边形叫做“等垂四边形”.
(1)如图①,四边形
 与四边形
与四边形 都是正方形,
都是正方形, ,求证:四边形
,求证:四边形 是“等垂四边形”;
是“等垂四边形”;(2)如图②,四边形
 是“等垂四边形”,
是“等垂四边形”, ,连接
,连接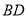 ,点
,点 ,
, ,
, 分别是AD,BC,BD的中点,连接EG,FG,EF.试判定
分别是AD,BC,BD的中点,连接EG,FG,EF.试判定 的形状,并证明;
的形状,并证明;(3)如图③,四边形
 是“等垂四边形”,
是“等垂四边形”, ,
,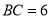 ,试求边AB长的最小值.
,试求边AB长的最小值.


-
科目: 来源: 题型:
查看答案和解析>>【题目】小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.有下列结论;①A,B两城相距300 km;②小路的车比小带的车晚出发1 h,却早到1 h;③小路的车出发后2.5 h追上小带的车;④当小带和小路的车相距50 km时,t=
 或t=
或t= .其中正确的结论有( )
.其中正确的结论有( )
A. ①②③④B. ①②④
C. ①②D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,△ABC及AC边的中点O。
求作:平行四边形ABCD。

小敏的作法如下:
①连接BO并延长,在延长线上截取OD=BO;
②连接DA,DC.

所以四边形ABCD就是所求作的平行四边形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是_________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形 ABCD中AB= 3,点B在边CD上,且 CD=3DE. 将△ADE沿AE对折至△AFE,延长EF交边BC 于点G,连接AG,CF下列结论:①点G是BC的中点;②FG=FC;③
 GAE=45;④GE=BG+DE.其中正确的是( )
GAE=45;④GE=BG+DE.其中正确的是( )
A. ①② B. ①③④ C. ②③ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有三个球,其中2个红球,1个白球,它们除颜色不同外其余都相同:
(1)摸出一个球记下颜色后放回,并搅匀,再摸出一个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(2)现再将n个白球放入布袋中搅匀后使摸出一个球是白球的概率为
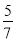 ,求n的值.
,求n的值.
相关试题

