【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() ,与
,与![]() 轴交于
轴交于![]() .
.
(1)若![]() ,求抛物线的解析式,并写出抛物线的对称轴;
,求抛物线的解析式,并写出抛物线的对称轴;
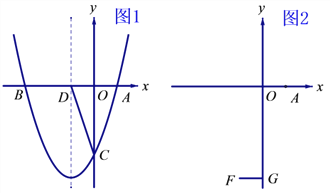
(2)如图1,在(1)的条件下,设抛物线的对称轴交轴于![]() ,在对称轴左侧的抛物线上有一点
,在对称轴左侧的抛物线上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
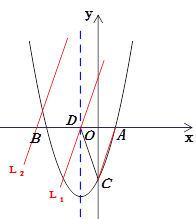
(3)如图2,设![]() ,
, ![]() 于
于![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线的解析式为:y=x2+2x-3,对称轴为:x=-1;(2)点E坐标为(-4,5);(3)m的取值范围是:-4≤m≤4,且m≠0.
【解析】试题分析:(1)利用待定系数法即可得解析式,再根据抛物线对称轴公式即可得对称轴;
(2)先求出AC的解析式,然后求出过点D与AC平行的直线解析式,即可得到直线AC向上平移了6个单位长度,再根据![]() 可知点E为直线AC向上平移20个单位长度后与抛物线的交点,联立解析式解方程组即可得;
可知点E为直线AC向上平移20个单位长度后与抛物线的交点,联立解析式解方程组即可得;
(3)分m>0、m<0两种情况进行讨论即可得.
试题解析:(1)∵![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() ,m=-3,
,m=-3,
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为:y=x2+2x-3,
对称轴为:x=-1;
(2)∵点A(1,0),C(0,-3),
∴直线AC为y= 3x-3,
∴过点D(-1,0)且平行于AC的直线ll为:y= 3x+3,
∴直线AC向上平移6个单位得到直线l1,
∴将直线AC向上平移![]() 个单位得到直线l2:y=3x+17,
个单位得到直线l2:y=3x+17,
联立方程组, ![]() ,
,
解得, ![]() ,
, ![]() (不合题意,舍去),
(不合题意,舍去),
∴点E坐标为(-4,5);
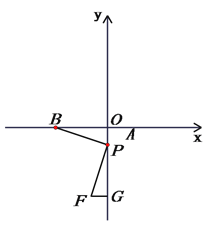
(3)设点P(0,y),
①当m<0时,如图所示,易证△POB~△FPG,得![]() ,
,
∴![]() ,
,
∴m=y2+4y=(y+2)2-4,
∵-4<y<0,
∴-4≤m<0;
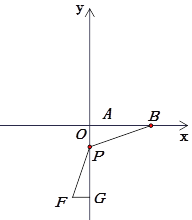
②当m>0时,如图所示,易证△POB~△FPG,得![]() ,
,
∴![]() ,
,
∴m= -y2 -4y= -(y+2)2+4,
∵-4<y<0,
∴0<m≤4,
综上所述,m的取值范围是:-4≤m≤4,且m≠0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在崇仁一中中学生篮球赛中,小方共打了10场球.他在第6,7,8,9场比赛中分别得了22,15,12和19分,他的前9场比赛的平均得分y比前5场比赛的平均得分x要高 .如果他所参加的10场比赛的平均得分超过18分
(1)用含x的代数式表示y;
(2)小方在前5场比赛中,总分可达到的最大值是多少?
(3)小方在第10场比赛中,得分可达到的最小值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=
 ,AN=
,AN= ,求圆O的直径的长度.
,求圆O的直径的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.

(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一组对边相等目这一组对边所在直线互相垂直的凸四边形叫做“等垂四边形”.
(1)如图①,四边形
 与四边形
与四边形 都是正方形,
都是正方形, ,求证:四边形
,求证:四边形 是“等垂四边形”;
是“等垂四边形”;(2)如图②,四边形
 是“等垂四边形”,
是“等垂四边形”, ,连接
,连接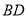 ,点
,点 ,
, ,
, 分别是AD,BC,BD的中点,连接EG,FG,EF.试判定
分别是AD,BC,BD的中点,连接EG,FG,EF.试判定 的形状,并证明;
的形状,并证明;(3)如图③,四边形
 是“等垂四边形”,
是“等垂四边形”, ,
,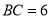 ,试求边AB长的最小值.
,试求边AB长的最小值.


-
科目: 来源: 题型:
查看答案和解析>>【题目】小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.有下列结论;①A,B两城相距300 km;②小路的车比小带的车晚出发1 h,却早到1 h;③小路的车出发后2.5 h追上小带的车;④当小带和小路的车相距50 km时,t=
 或t=
或t= .其中正确的结论有( )
.其中正确的结论有( )
A. ①②③④B. ①②④
C. ①②D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班级为准备元旦联欢会,欲购买价格分别为2元、4元和10元的三种奖品,每种奖品至少购买一件,共买16件,恰好用50元.若2元的奖品购买a件.
(1)用含a的代数式表示另外两种奖品的件数;
(2)请你设计购买方案,并说明理由.
相关试题

