【题目】如图,正方形OAPB、ADFE的顶点A、D. B在坐标轴上,点B在AP上,点P、F在函数![]() 上,已知正方形OAPB的面积是9.
上,已知正方形OAPB的面积是9.

(1)求k的值和直线OP的解析式;
(2)求正方形ADFE的边长
(3)函数![]() 在第三象限的图像上是否存在一点Q,使得△ABQ的面积为10.5?若存在,求出Q点坐标;若不存在,请说明理由.
在第三象限的图像上是否存在一点Q,使得△ABQ的面积为10.5?若存在,求出Q点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;直线OP的解析式为y=x;(2)正方形ADFE的边长为得
;直线OP的解析式为y=x;(2)正方形ADFE的边长为得![]() ;(3)不存在.
;(3)不存在.
【解析】
(1)利用正方形的性质得到P点坐标为(3,3),再把P点坐标代入![]() 即可得到k的值;然后利用待定系数法求直线OP的解析式;
即可得到k的值;然后利用待定系数法求直线OP的解析式;
(2)设正方形ADFE的边长为a,利用正方形的性质易表示F点的坐标为(a+3,a),然后把F(a+3,a)代入![]() ,再解关于a的一元二次方程即可得到正方形ADFE的边长;
,再解关于a的一元二次方程即可得到正方形ADFE的边长;
(3)如图,连接QA,QB,QO,AB,设Q(x,y)(x<0),利用S△ABQ=S△AOQ+ S△BOQ+ S△ABO=10.5列出关于x的方程求解即可.
(1)∵正方形OAPB的面积为9,
∴PA=PB=3,
∴P点坐标为(3,3),
把P(3,3)代入![]() 得,k=3×3=9,
得,k=3×3=9,
即![]() ;
;
设直线OP的解析式为y=k1x,
把P(3,3)代入y=k1x得,k1=1,
∴直线OP的解析式为y=x;
(2)设正方形ADFE的边长为a,则F点的坐标为(a+3,a),
把F(a+3,a)代入![]() 得,a(a+3)=9,解得a1=
得,a(a+3)=9,解得a1=![]() ,a2=
,a2=![]() ,
,
∴正方形ADFE的边长为得![]() ;
;
(3)∵P(3,3)且四边形AOBP是正方形,
∴AO=BO=3,
设Q(x,![]() )(x<0),连接QO,QB,QA,AB,如图所示,
)(x<0),连接QO,QB,QA,AB,如图所示,
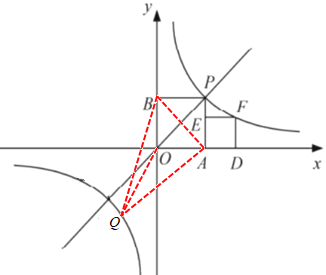
假定△ABQ的面积为10.5,则有,
S△BOQ+S△AOQ+S△AOB=10.5
即,![]()
∵x<0
∴方程整理得,![]()
∵△=![]()
∴此方程无实数解,
故函数![]() 在第三象限的图像上不存在一点Q,使得△ABQ的面积为10.5
在第三象限的图像上不存在一点Q,使得△ABQ的面积为10.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天爷爷和小强去爬山,小强让爷爷先上, 图中两条线段分别表示两人离开山脚的距离
 (米)与爬山所用时间
(米)与爬山所用时间 (分)的关系,看图回答问题:
(分)的关系,看图回答问题:
①小强让爷爷先上______米,________ (填“小强”或“爷爷") 先爬上山顶;
②求小强离开山脚的距离
 (米)与爬山所用时间
(米)与爬山所用时间 (分)的函数解析式及定义域;
(分)的函数解析式及定义域; ③爷爷的平均速度为_______米/分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 ,则下列关于该函数的描述中,错误的是( )
,则下列关于该函数的描述中,错误的是( )A. 该函数的最小值是
B. 该函数图象与
 轴没有交点
轴没有交点C. 该函数图象与
 轴有两个不同的交点
轴有两个不同的交点D. 当
 时,
时, 随着
随着 的增大而增大
的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中,正比例函数
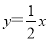 图像与反比例函数
图像与反比例函数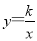 交于点A(4,
交于点A(4,  ),过点A作
),过点A作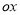 的垂线交x轴于点B.
的垂线交x轴于点B.
(1)求反比例函数的解析式;
(2)如果点C在
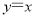 的图像上,且△CAB的面积为△OAB面积的2倍,求点C的坐标.
的图像上,且△CAB的面积为△OAB面积的2倍,求点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是________(填A或B或C)
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值
②计算:(1-
 )(1-
)(1- )(1-
)(1- )…(1-
)…(1- )(1-
)(1- )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
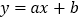 的图象与
的图象与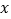 轴、
轴、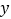 轴交于
轴交于 、
、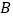 两点,与反比例函数
两点,与反比例函数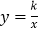 的图象相交于
的图象相交于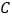 、
、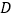 两点,分别过
两点,分别过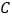 、
、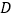 两点作
两点作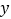 轴,
轴,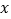 轴的垂线,垂足为
轴的垂线,垂足为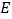 、
、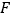 ,连接
,连接 、
、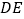 ,有下列结论:①
,有下列结论:①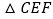 与
与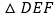 的面积相等;②
的面积相等;② ;③
;③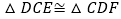 ;④
;④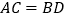 ;⑤
;⑤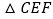 的面积等于
的面积等于 ,其中正确的个数有( )
,其中正确的个数有( )
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
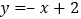 分别与
分别与 轴,
轴,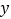 轴交于
轴交于 ,
, 两点,与双曲线
两点,与双曲线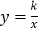 交于
交于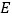 ,
,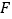 两点,若
两点,若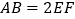 ,则
,则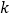 的值是________.
的值是________.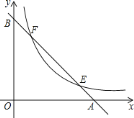
相关试题

