【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,分别过
两点,分别过![]() 、
、![]() 两点作
两点作![]() 轴,
轴,![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() 、
、![]() ,连接
,连接![]() 、
、![]() ,有下列结论:①
,有下列结论:①![]() 与
与![]() 的面积相等;②
的面积相等;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 的面积等于
的面积等于![]() ,其中正确的个数有( )
,其中正确的个数有( )
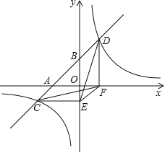
A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】C
【解析】
此题要根据反比例函数的性质进行求解,解决此题的关键是要证出CD∥EF,可从①问的面积相等入手;△DFE中,以DF为底,OF为高,可得S△DFE=![]() |xD||yD|=
|xD||yD|=![]() 2k,同理可求得△CEF的面积也是
2k,同理可求得△CEF的面积也是![]() k,因此两者的面积相等;若两个三角形都以EF为底,那么它们的高相同,即E、F到AD的距离相等,由此可证得CD∥EF,然后根据这个条件来逐一判断各选项的正误.
k,因此两者的面积相等;若两个三角形都以EF为底,那么它们的高相同,即E、F到AD的距离相等,由此可证得CD∥EF,然后根据这个条件来逐一判断各选项的正误.
设点D的坐标为(x,![]() ),则F(x,0).
),则F(x,0).
由函数的图象可知:x>0,k>0.
∴S△DFE=![]() DFOF=
DFOF=![]() |xD||yD|=
|xD||yD|=![]() k,
k,
同理可得S△CEF=![]() k,故⑤正确;
k,故⑤正确;
故S△DEF=S△CEF.故①正确;
若两个三角形以EF为底,则EF边上的高相等,故CD∥EF.故②正确;
③条件不足,无法得到判定两三角形全等的条件,故③错误;
④∵CD∥EF,DF∥BE,
∴四边形DBEF是平行四边形,
∴S△DEF=S△BED,
同理可得S△ACF=S△ECF;
由①得:S△DBE=S△ACF.
又∵CD∥EF,BD、AC边上的高相等,
∴BD=AC,故④正确;
因此正确的结论有4个:①②④⑤.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中,正比例函数
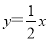 图像与反比例函数
图像与反比例函数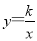 交于点A(4,
交于点A(4,  ),过点A作
),过点A作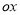 的垂线交x轴于点B.
的垂线交x轴于点B.
(1)求反比例函数的解析式;
(2)如果点C在
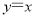 的图像上,且△CAB的面积为△OAB面积的2倍,求点C的坐标.
的图像上,且△CAB的面积为△OAB面积的2倍,求点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OAPB、ADFE的顶点A、D. B在坐标轴上,点B在AP上,点P、F在函数
 上,已知正方形OAPB的面积是9.
上,已知正方形OAPB的面积是9.
(1)求k的值和直线OP的解析式;
(2)求正方形ADFE的边长
(3)函数
 在第三象限的图像上是否存在一点Q,使得△ABQ的面积为10.5?若存在,求出Q点坐标;若不存在,请说明理由.
在第三象限的图像上是否存在一点Q,使得△ABQ的面积为10.5?若存在,求出Q点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是________(填A或B或C)
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值
②计算:(1-
 )(1-
)(1- )(1-
)(1- )…(1-
)…(1- )(1-
)(1- )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
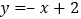 分别与
分别与 轴,
轴,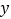 轴交于
轴交于 ,
, 两点,与双曲线
两点,与双曲线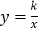 交于
交于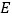 ,
,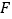 两点,若
两点,若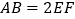 ,则
,则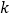 的值是________.
的值是________.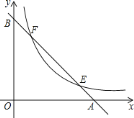
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品的进价为
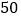 元,该产品的日销量
元,该产品的日销量 (件)是日销价
(件)是日销价 (元)的反比例函数,且当售价为每件
(元)的反比例函数,且当售价为每件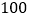 元时,每日可售出
元时,每日可售出 件,为获得日利润为
件,为获得日利润为 元,售价应定为________.
元,售价应定为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点
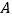 在双曲线
在双曲线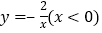 上,动点
上,动点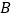 在双曲线
在双曲线 上,且直线
上,且直线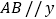 轴,若点
轴,若点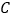 的坐标是
的坐标是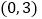 ,点
,点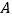 的横坐标为
的横坐标为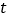 .
.
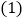 当
当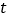 取不同的值时,
取不同的值时,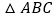 的面积________(填“变化”或者“不变化”);
的面积________(填“变化”或者“不变化”); 线段
线段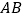 的长可以用
的长可以用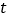 表示为________;
表示为________;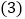 若点
若点 的坐标为
的坐标为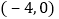 ,请问是否存在常数
,请问是否存在常数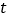 ,使得
,使得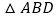 的面积等于
的面积等于 ?若有,请求出
?若有,请求出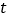 的值;若没有,请说明理由.
的值;若没有,请说明理由.
相关试题

