【题目】已知:一次函数y=3x﹣2的图象与某反比例函数的图象的一个公共点的横坐标为1.
(1)求该反比例函数的解析式;
(2)将一次函数y=3x﹣2的图象向上平移4个单位,求平移后的图象与反比例函数图象的交点坐标;
(3)请直接写出一个同时满足如下条件的函数解析式: ①函数的图象能由一次函数y=3x﹣2的图象绕点(0,﹣2)旋转一定角度得到;
②函数的图象与反比例函数的图象没有公共点.
参考答案:
【答案】
(1)解:把x=1代入y=3x﹣2,得y=1,
设反比例函数的解析式为 ![]() ,
,
把x=1,y=1代入得,k=1,
∴该反比例函数的解析式为 ![]()
(2)解:平移后的图象对应的解析式为y=3x+2,
解方程组 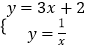 ,得
,得 ![]() 或
或 ![]() .
.
∴平移后的图象与反比例函数图象的交点坐标为( ![]() ,3)和(﹣1,﹣1)
,3)和(﹣1,﹣1)
(3)解:y=﹣2x﹣2.
(结论开放,常数项为﹣2,一次项系数小于﹣1的一次函数均可)
【解析】(1)先求出两函数的交点坐标,利用待定系数法即可求得反比例函数的解析式;(2)平移后的图象对应的解析式为y=3x+2,联立两函数解析式,进而求得交点坐标;(3)常数项为﹣2,一次项系数小于﹣1的一次函数均可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用
 ,
, ,
, ,
, …表示,则顶点
…表示,则顶点 的坐标是_____.
的坐标是_____.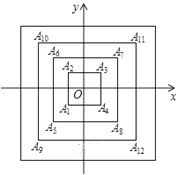
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了决定谁将获得仅有的一张科普报告入场券,甲和乙设计了如下的一个游戏: 口袋中有编号分别为1、2、3的红球三个和编号为4的白球一个,四个球除了颜色或编号不同外,没有任何别的区别,摸球之前将小球搅匀,摸球的人都蒙上眼睛.先甲摸两次,每次摸出一个球;把甲摸出的两个球放回口袋后,乙再摸,乙只摸一个球.如果甲摸出的两个球都是红色,甲得1分,否则,甲得0分;如果乙摸出的球是白色,乙得1分,否则,乙得0分;得分高的获得入场券,如果得分相同,游戏重来.
(1)运用列表或画树状图求甲得1分的概率;
(2)这个游戏是否公平?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明.

如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知)
且∠1=∠CGD(_______)
∴∠2=∠CGD(等量代换)
∴CE∥BF(_______)
∴∠_____=∠BFD(_______)
又∵∠B=∠C(已知)
∴∠BFD=∠B(_______)
∴AB∥CD(_______)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强在教学楼的点P处观察对面的办公大楼.为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米.求点P到AD的距离(用含根号的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b是正实数,那么,
 是恒成立的.
是恒成立的. 
(1)由 恒成立,说明
恒成立,说明  恒成立;
恒成立;
(2)已知a、b、c是正实数,由 恒成立,猜测:
恒成立,猜测: 
 也恒成立;
也恒成立;
(3)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明 恒成立.
恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】点A,点B在数轴上分别表示 6.5,x.点B在点A的左边,且点A,点B之间有9个整数,则x的取值范围为_____.
相关试题

