【题目】(本题8分) 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲 在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式 ![]() ,已知点O与球网的水平距离为5m,球网的高度1.55m.
,已知点O与球网的水平距离为5m,球网的高度1.55m.
(1)当a= ![]() 时,①求h的值.②通过计算判断此球能否过网.
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
参考答案:
【答案】
(1)
解:①∵a=![]() ,P(0,1);
,P(0,1);
∴1=![]() +h;
+h;
∴h=![]() ;
;
②把x=5代入y=![]() 得:
得:
y=![]() =1.625;
=1.625;
∵1.625>1.55;
∴此球能过网.
(2)
解:把(0,1),(7, ![]() )代入y=a
)代入y=a![]() 得:;
得:;
![]() ;解得:
;解得: ;
;
∴a=![]() .
.
【解析】(1)①利用a=![]() ,将点(0,1)代入解析式即可求出h的值;②利用x=5代入解析式求出y,再与1.55比较大小即可判断是否过网;
,将点(0,1)代入解析式即可求出h的值;②利用x=5代入解析式求出y,再与1.55比较大小即可判断是否过网;
(2)将点(0,1),(7,![]() )代入解析式得到一个二元一次方程组求解即可得出a的值。
)代入解析式得到一个二元一次方程组求解即可得出a的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A、B、C、D四个等级,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题:

(1)抽取了__名学生成绩;
(2)请把频数分布直方图补充完整;
(3)扇形统计图中A等级所在的扇形的圆心角度数是__;
(4)若A、B、C三个等级为合格,该校初二年级有900名学生,估计全年级生物合格的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有颜色不同的黄、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复

 下表是活动中的一组统计数据:
下表是活动中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近______;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请你设计一个增(减)袋中白球或黄球球个数的方案,使得从袋中摸出一个球,这只球是黄球的概率大于是白球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用火柴棒按下列方式搭三角形:

(1)填写下面表
三角形个数
1
2
3
4
…
火柴棒根数
…
(2)搭10个这样的三角形需要 根火柴棒.
(3)搭n个这样的三角形需要 根火柴棒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+
 x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).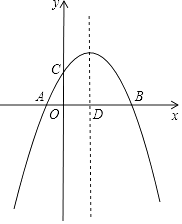
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,S△ADE=8,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.

(1)求证:DE是⊙O的切线;
(2)当AB=4 ,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
相关试题

