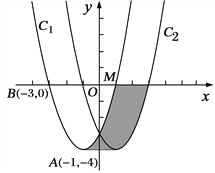
【题目】如图,在平面直角坐标xOy中,抛物线![]() 的顶点为A(-1,-4),且过点B(-3,0)
的顶点为A(-1,-4),且过点B(-3,0)
(1)将抛物线![]() 向右平移2个单位得抛物线
向右平移2个单位得抛物线![]() ,设C2的解析式为y=ax2+bx+c,求a,b,c的值;
,设C2的解析式为y=ax2+bx+c,求a,b,c的值;
(2)在(1)的条件下,直接写出ax2+bx+c>5的解集_________________
(3)写出阴影部分的面积![]() =_____________.
=_____________.
参考答案:
【答案】(1)a,b,c的值分别为1,-2,-3;(2)x<-2或x>4;(3)8.
【解析】(1)设抛物线C1的解析式为y=a(x+1)2-4,将B点代入解析式,求a,再由平移的规律得出C2的解析式,从而得出a,b,c的值;
(2)令y=5,得出x的值,根据图象得出ax2+bx+c>5的解集.
(3)阴影部分可以转换成求平行四边形的面积,即函数图象平移的距离乘以A点纵坐标的绝对值.
(1)设抛物线C1的解析式为y=a(x+1)2-4,
将点B(-3,0)代入得a=1,
∴抛物线的解析式为y=(x+1)2-4,
∵将抛物线C1向右平移2个单位得抛物线C2,
∴抛物线C2的解析式为y=(x-1)2-4,
∴a,b,c的值分别为1,-2,-3;
(2)令y=(x-1)2-4中y=5,得x=4或-2.
∴x<-2或x>4时,ax2+bx+c>5,
即ax2+bx+c>5的解集为x<-2或x>4;
(3)阴影部分可以转换成求平行四边形的面积,S=2×|yA|=2×4=8,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,O,B三点在同一直线上,∠BOD与∠BOC互补.
(1)∠AOC与∠BOD的度数相等吗,为什么?
(2)已知OM平分∠AOC,若射线ON在∠COD的内部,且满足∠AOC与∠MON互余;
①∠AOC=32°,求∠MON的度数;
②试探究∠AON与∠DON之间有怎样的数量关系,请写出结论并说明理由.

-
科目: 来源: 题型:
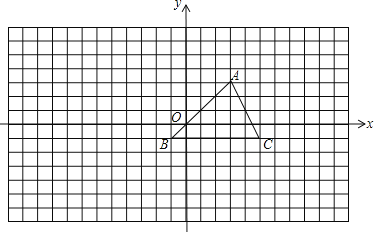
查看答案和解析>>【题目】如图,方格中的每个小方格都是边长为1的正方形,我们把以格点间的连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得△A2B2C2,画出△A2B2C2的图形并写出B2的坐标;
(3)把△ABC以点A为位似中心放大,使放大前后对应边的比为1∶2,画出△AB3C3的图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=ax2+bx+c, y与x的一些对应值如下表:
x
……
1
0
1
2
3
4
……
ax2+bx+c
……
3
1
3
……
(1)根据表格中的数据,确定二次函数解析式为_________________;
(2)填齐表格中空白处的对应值并利用上表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当 1 < x ≤4时,y的取值范围是_________________;

-
科目: 来源: 题型:
查看答案和解析>>【题目】有以下运算程序,如图所示:

比如,输入数对(2,1),输出W=2.
(1)若输入数对(1,﹣2),则输出W= ;
(2)分别输入数对(m,﹣n)和(﹣n,m),输出的结果分别是W1,W2,试比较W1,W2的大小,并说明理由;
(3)设a=|x﹣2|,b=|x﹣3|,若输入数对(a,b)之后,输出W=26,求a+b的值.
-
科目: 来源: 题型:
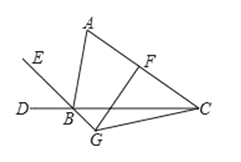
查看答案和解析>>【题目】如图 ,BE平分△ABC的外角∠ABD,F是 AC的中点,过 F点作 AC的垂线交 BE的反向延长线于 G点, 连 EG.若∠ABC=80°,则∠ACG的度数为是_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
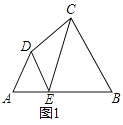
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:

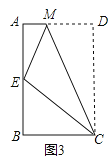
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
相关试题

