【题目】如图,A,O,B三点在同一直线上,∠BOD与∠BOC互补.
(1)∠AOC与∠BOD的度数相等吗,为什么?
(2)已知OM平分∠AOC,若射线ON在∠COD的内部,且满足∠AOC与∠MON互余;
①∠AOC=32°,求∠MON的度数;
②试探究∠AON与∠DON之间有怎样的数量关系,请写出结论并说明理由.

参考答案:
【答案】(1)∠AOC=∠BOD,理由详见解析;(2)① 58°;②∠AON=∠DON,理由详见解析.
【解析】
(1)根据补角的性质即可求解;
(2)①根据余角的定义解答即可;
②根据角平分线的定义以及补角与余角的定义,分别用∠AOM的代数式表示出∠AON与∠DON即可解答.
解:(1)∠AOC=∠BOD,
∵∠BOD与∠BOC互补,
∴∠BOD+∠BOC=180°,
∵∠AOC+∠BOC=180°,
∴∠AOC=∠BOD;
(2)①∵∠AOC与∠MON互余,
∴∠MON=90°﹣∠AOC=58°;
②∠AON=∠DON,
理由如下:
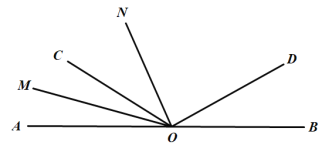
∵OM平分∠AOC,
∴∠AOC=2∠AOM,∠COM=∠AOM,
∵∠AOC与∠MON互余,
∴∠AOC+∠MON=90°,
∴∠AON=90°﹣∠AOM,
∴∠CON=90°﹣3∠AOM,
∵∠BOD与∠BOC互补,
∴∠BOD+∠BOC=180°,
∴∠CON+∠DON+2∠BOD=180°,
又∵∠BOD=∠AOC=2∠AOM,
∴∠DON=180°﹣∠CON﹣2∠BOD
=180°﹣(90°﹣3∠AOM)﹣4∠AOM
=90°﹣∠AOM.
∴∠AON=∠DON.
-
科目: 来源: 题型:
查看答案和解析>>【题目】AD为△ABC边上 BC上的中线,若 AD=4,AC=5,则 AB的取值范围是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
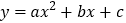 的图象与x轴交于(
的图象与x轴交于(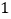 , 0)和(
, 0)和(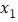 , 0), 其中
, 0), 其中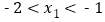 ,与
,与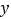 轴交于正半轴上一点.下列结论:①
轴交于正半轴上一点.下列结论:① ;②
;②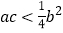 ;③a>b;④
;③a>b;④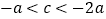 .其中正确结论的序号是____________.
.其中正确结论的序号是____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】有三条长度均为a的线段,分别按以下要求画圆.
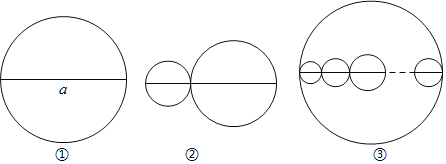
(1)如图①,以该线段为直径画一个圆,记该圆的周长为C1;如图②,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为C2,请指出C1和C2的数量关系,并说明理由;
(2)如图③,当a=11时,以该线段为直径画一个大圆,再在大圆内画若千小圆,这些小圆的直径都和大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有小圆的周长的和为 .(直接填写答案,结果保留π)
-
科目: 来源: 题型:
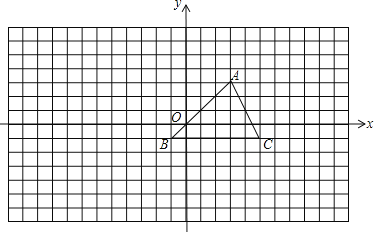
查看答案和解析>>【题目】如图,方格中的每个小方格都是边长为1的正方形,我们把以格点间的连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得△A2B2C2,画出△A2B2C2的图形并写出B2的坐标;
(3)把△ABC以点A为位似中心放大,使放大前后对应边的比为1∶2,画出△AB3C3的图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=ax2+bx+c, y与x的一些对应值如下表:
x
……
1
0
1
2
3
4
……
ax2+bx+c
……
3
1
3
……
(1)根据表格中的数据,确定二次函数解析式为_________________;
(2)填齐表格中空白处的对应值并利用上表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当 1 < x ≤4时,y的取值范围是_________________;

-
科目: 来源: 题型:
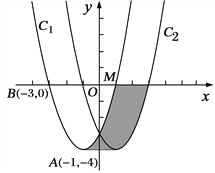
查看答案和解析>>【题目】如图,在平面直角坐标xOy中,抛物线
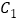 的顶点为A(-1,-4),且过点B(-3,0)
的顶点为A(-1,-4),且过点B(-3,0)(1)将抛物线
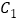 向右平移2个单位得抛物线
向右平移2个单位得抛物线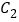 ,设C2的解析式为y=ax2+bx+c,求a,b,c的值;
,设C2的解析式为y=ax2+bx+c,求a,b,c的值; (2)在(1)的条件下,直接写出ax2+bx+c>5的解集_________________
(3)写出阴影部分的面积
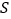 =_____________.
=_____________.
相关试题

