【题目】有以下运算程序,如图所示:
![]()
比如,输入数对(2,1),输出W=2.
(1)若输入数对(1,﹣2),则输出W= ;
(2)分别输入数对(m,﹣n)和(﹣n,m),输出的结果分别是W1,W2,试比较W1,W2的大小,并说明理由;
(3)设a=|x﹣2|,b=|x﹣3|,若输入数对(a,b)之后,输出W=26,求a+b的值.
参考答案:
【答案】(1)1;(2)W1=W2,理由详见解析;(3)51 .
【解析】
(1)把a=1,b=﹣2输入运算程序,计算即可;
(2)按照计算程序分别求出W1,W2的值再进行比较.
(3)分四种情况:当![]() 时,当
时,当![]() 时,当
时,当![]() 时,当
时,当![]() 时,分情况讨论x在不同的取值范围内输出值为26,求出符合条件的x的值,再计算a+b的值.
时,分情况讨论x在不同的取值范围内输出值为26,求出符合条件的x的值,再计算a+b的值.
解:(1)输入数对(1,﹣2),即a=1,b=﹣2,
W=[|a﹣b|+(a+b)]×![]() =1
=1
故答案为1.
(2)当a=m,b=﹣n时,W1=[|a﹣b|+(a+b)]×![]() =
=![]() [|m+n|+(m﹣n)]
[|m+n|+(m﹣n)]
当a=﹣n,b=m时,W2=[|a﹣b|+(a+b)]×![]() =[|﹣n﹣m|+(m﹣n)]×
=[|﹣n﹣m|+(m﹣n)]×![]() =
=![]() [|m+n|+(m﹣n)]
[|m+n|+(m﹣n)]
即W1=W2
(3)设a=|x﹣2|,b=|x﹣3|,若输入数对(a,b)之后,输出W.
![]()
当![]() 时,
时,![]()
∴![]()
解得![]()
![]()
当![]() 时,
时,![]()
∴![]()
解得![]() (不符合题意,舍去)
(不符合题意,舍去)
当![]() 时,
时,![]()
∴![]()
解得![]() (不符合题意,舍去)
(不符合题意,舍去)
当![]() 时,
时,![]()
∴![]()
解得![]()
![]()
综上所述,a+b的值为51.
-
科目: 来源: 题型:
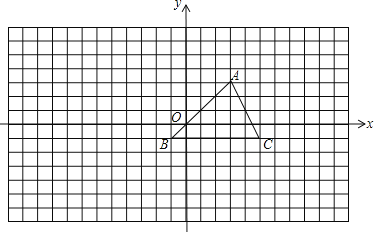
查看答案和解析>>【题目】如图,方格中的每个小方格都是边长为1的正方形,我们把以格点间的连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得△A2B2C2,画出△A2B2C2的图形并写出B2的坐标;
(3)把△ABC以点A为位似中心放大,使放大前后对应边的比为1∶2,画出△AB3C3的图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=ax2+bx+c, y与x的一些对应值如下表:
x
……
1
0
1
2
3
4
……
ax2+bx+c
……
3
1
3
……
(1)根据表格中的数据,确定二次函数解析式为_________________;
(2)填齐表格中空白处的对应值并利用上表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当 1 < x ≤4时,y的取值范围是_________________;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标xOy中,抛物线
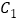 的顶点为A(-1,-4),且过点B(-3,0)
的顶点为A(-1,-4),且过点B(-3,0)(1)将抛物线
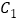 向右平移2个单位得抛物线
向右平移2个单位得抛物线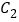 ,设C2的解析式为y=ax2+bx+c,求a,b,c的值;
,设C2的解析式为y=ax2+bx+c,求a,b,c的值; (2)在(1)的条件下,直接写出ax2+bx+c>5的解集_________________
(3)写出阴影部分的面积
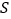 =_____________.
=_____________.
-
科目: 来源: 题型:
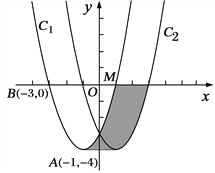
查看答案和解析>>【题目】如图 ,BE平分△ABC的外角∠ABD,F是 AC的中点,过 F点作 AC的垂线交 BE的反向延长线于 G点, 连 EG.若∠ABC=80°,则∠ACG的度数为是_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
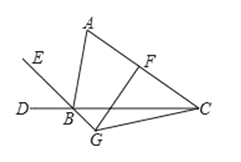
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:

(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
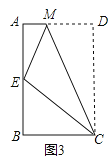
-
科目: 来源: 题型:
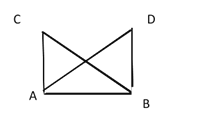
查看答案和解析>>【题目】如图,海岸上有 A,B 两个观测点,点 B 在点 A 的正东方,海岛 C 在观测点 A 的正北方, 海岛 D 在观测点 B 的正北方。如果从观测点 A 看海岛 C,D 的视角∠CAD 与从观测点 B 海岛 C,D 的视角∠CBD 相等,那么海岛 C,D 到观测点 A,B 所在海岸的距离 CA,DB 相等,请说明理由。
相关试题

