【题目】阅读理解:
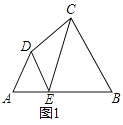
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:

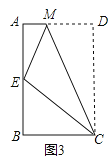
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
参考答案:
【答案】解:(1)点E是四边形ABCD的边AB上的相似点。理由如下:
∵∠A=55°,∴∠ADE+∠DEA=125°。
∵∠DEC=55°,∴∠BEC+∠DEA=125°。
∴∠ADE=∠BEC。
∵∠A=∠B,∴△ADE∽△BEC。
∴点E是四边形ABCD的AB边上的相似点。
(2)作图如下:

(3)∵点E是四边形ABCM的边AB上的一个强相似点,
∴△AEM∽△BCE∽△ECM。∴∠BCE=∠ECM=∠AEM。
由折叠可知:△ECM≌△DCM,∴∠ECM=∠DCM,CE=CD。
∴∠BCE=![]() ∠BCD=30°。∴BE=
∠BCD=30°。∴BE=![]() CE=
CE=![]() AB。
AB。
在Rt△BCE中,![]() ,
,
∴![]() ,∴
,∴![]() 。
。
【解析】
试题(1)要证明点E是四边形ABCD的AB边上的相似点,只要证明有一组三角形相似就行,很容易证明△ADE∽△BEC,所以问题得解。
(2)根据两个直角三角形相似得到强相似点的两种情况即可。
(3)因为点E是梯形ABCD的AB边上的一个强相似点,所以就有相似三角形出现,根据相似三角形的对应线段成比例,可以判断出AE和BE的数量关系,从而可求出解。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标xOy中,抛物线
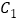 的顶点为A(-1,-4),且过点B(-3,0)
的顶点为A(-1,-4),且过点B(-3,0)(1)将抛物线
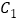 向右平移2个单位得抛物线
向右平移2个单位得抛物线 ,设C2的解析式为y=ax2+bx+c,求a,b,c的值;
,设C2的解析式为y=ax2+bx+c,求a,b,c的值; (2)在(1)的条件下,直接写出ax2+bx+c>5的解集_________________
(3)写出阴影部分的面积
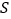 =_____________.
=_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有以下运算程序,如图所示:

比如,输入数对(2,1),输出W=2.
(1)若输入数对(1,﹣2),则输出W= ;
(2)分别输入数对(m,﹣n)和(﹣n,m),输出的结果分别是W1,W2,试比较W1,W2的大小,并说明理由;
(3)设a=|x﹣2|,b=|x﹣3|,若输入数对(a,b)之后,输出W=26,求a+b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,BE平分△ABC的外角∠ABD,F是 AC的中点,过 F点作 AC的垂线交 BE的反向延长线于 G点, 连 EG.若∠ABC=80°,则∠ACG的度数为是_____
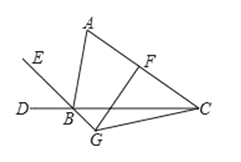
-
科目: 来源: 题型:
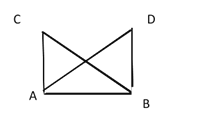
查看答案和解析>>【题目】如图,海岸上有 A,B 两个观测点,点 B 在点 A 的正东方,海岛 C 在观测点 A 的正北方, 海岛 D 在观测点 B 的正北方。如果从观测点 A 看海岛 C,D 的视角∠CAD 与从观测点 B 海岛 C,D 的视角∠CBD 相等,那么海岛 C,D 到观测点 A,B 所在海岸的距离 CA,DB 相等,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.
求证:AD+BC=AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件)
100
110
120
130
…
月销量(件)
200
180
160
140
…
已知该运动服的进价为每件60元,设售价为
 元.
元.(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为
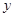 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?
相关试题

