【题目】△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠DCA的平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

参考答案:
【答案】(1)证明见解析;(2)(2)当点O运动到AC中点时,四边形AECF是矩形;理由见解析.
【解析】试题分析:(1)由于CE平分∠BCA,那么有∠1=∠2,而MN∥BC,利用平行线的性质有∠1=∠3,等量代换有∠2=∠3,于OE=OC,同理OC=OF,于是OE=OF;(2)OA=OC,那么可证四边形AECF是平行四边形,又CE、CF分别是∠BCA及其外角的角平分线,易证∠ECF是90°,从而可证四边形AECF是矩形.
(1)∵CE平分∠BCA,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO;
(2)当点O运动到AC中点时,四边形AECF是矩形;理由如下:如图所示:

∵OA=OC,
∴四边形AECF是平行四边形,
∵CF是∠BCA的外角平分线,
∴∠4=∠5,
又∵∠1=∠2,
∴∠1+∠5=∠2+∠4,
又∵∠1+∠5+∠2+∠4=180°,
∴∠2+∠4=90°,
∴平行四边形AECF是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(x﹣2)2=3(x﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点(﹣2,5),并且与y轴交于点P,直线y=
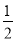 x+3与y轴交于点Q,点Q恰与点P关于x轴对称,求这个一次函数的解析式.
x+3与y轴交于点Q,点Q恰与点P关于x轴对称,求这个一次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;

(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b互为倒数,c,d互为相反数,x的绝对值等于2,则ab﹣(c+d)+x2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-5, 6)与点A关于x轴对称,则点A的坐标为;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a+b=3,ab=4,那么a2+b2的值是_.
相关试题

