【题目】定义:如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“直观三角形”.
(1)抛物线y=x2![]() 的“直观三角形”是 .
的“直观三角形”是 .
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
(2)若抛物线y=ax2+2ax﹣3a的“直观三角形”是直角三角形,求a的值;
(3)如图,面积为12![]() 的矩形ABCO的对角线OB在x轴的正半轴上,AC与OB相交于点E,若△ABE是抛物线y=ax2+bx+c的“直观三角形”,求此抛物线的解析式.
的矩形ABCO的对角线OB在x轴的正半轴上,AC与OB相交于点E,若△ABE是抛物线y=ax2+bx+c的“直观三角形”,求此抛物线的解析式.

参考答案:
【答案】(1)B;(2)a=±![]() ;(3)抛物线的解析式y=﹣x2+6
;(3)抛物线的解析式y=﹣x2+6![]() x﹣24.
x﹣24.
【解析】
按照题目中给定的“直观三角形”定义,求解,(1)证明三角形是等边三角形.(2)利用三角形是直角三角形反推a.(3)利用已知条件,列方程组求二次函数的解析式.
解:(1)设抛物线y=x2﹣2![]() x与x轴的交点坐标为A,B,顶点为D,
x与x轴的交点坐标为A,B,顶点为D,
∴A(0,0),B(2![]() ,0),D(
,0),D(![]() ,﹣3),
,﹣3),
∴AD=BD=2![]() ,AB=2
,AB=2![]() ,
,
∴AB=AD=BD,
∴△ABD是等边三角形,
∴抛物线y=x2﹣2![]() x对应的“直观三角形”是等边三角形,
x对应的“直观三角形”是等边三角形,
故答案为:B;
(2)设抛物线y=ax2+2ax﹣3a与x轴的交点坐标为A,B,顶点为D,∴A(﹣3,0),B(1,0),D(﹣1,﹣4a),
∵抛物线y=ax2+2ax﹣3a对应的“直观三角形”是直角三角形,
∴AB2=AD2+BD2,
∴16=4+16a2+4+16a2,
∴a=±![]() ;
;
(3)如图,
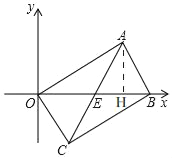
∵四边形ABCD是矩形,
∴AE=CE=OE=BE,
∴S△ABE=![]() S矩形ABCD=
S矩形ABCD=![]() ×12
×12![]() =3
=3![]() ,
,
∵△ABE是抛物线的“直观三角形”,
根据抛物线的对称性得,AE=AB,
∴AE=AB=BE,
∴△ABE是等边三角形,
过点A作AH⊥BE,
∴AH=ABsin∠ABE=![]() AB=
AB=![]() BE,
BE,
∴![]() BE2=3
BE2=3![]() ,
,
∴BE=2![]() ,
,
∴AH=3,EH=![]() ,
,
∴A(3![]() ,3),E(2
,3),E(2![]() ,0),B(4
,0),B(4![]() ,0),
,0),
设抛物线解析式为y=a(x﹣3![]() )2+3,
)2+3,
将点E(2![]() ,0)代入得,a=﹣1,
,0)代入得,a=﹣1,
∴y=﹣(x﹣3![]() )2+3=﹣x2+6
)2+3=﹣x2+6![]() x﹣24.
x﹣24.
∴过点A,B,E三点的抛物线的解析式y=﹣x2+6![]() x﹣24.
x﹣24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E,连接BD,DE,若∠A=30°,AB=AC,则∠BDE的度数为( ).

A.52.5°B.60°C.67.5°D.75°
-
科目: 来源: 题型:
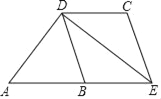
查看答案和解析>>【题目】如图,已知在△ADE中,∠ADE=90°,点B是AE的中点,过点D作DC∥AE,DC=AB,连结BD、CE.
(1)求证:四边形BDCE是菱形;
(2)若AD=8,BD=6,求菱形BDCE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,P为底边BC上任意点,过P作两腰的平行线分别与AB,AC相交于Q,R两点,又P′是P关于直线RQ的对称点,证明:P′在△ABC的外接圆上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=
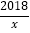 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,过B作⊙O的切线,在该切线上取点C,连接AC交⊙O于D,若⊙O的半径是6,∠C=36°,则劣弧AD的长是( )

A.
 B.
B.  C.
C.  D. 3π
D. 3π
相关试题

