【题目】对于边长为4的等边三角形ABC,以点B为坐标原点,底边BC方向所在的直线为x轴正方向,建立平面直角坐标系,则顶点A的坐标是 .
参考答案:
【答案】(2,2![]() )或(2,﹣2
)或(2,﹣2![]() )
)
【解析】
试题分析:分类讨论:
当点C在第一象限,如图1,作AD⊥BC于D,根据等边三角形的性质得BD=CD=![]() BC=2,∠BAD=30°,再利用含30度的直角三角形三边的关系得到AD=
BC=2,∠BAD=30°,再利用含30度的直角三角形三边的关系得到AD=![]() BD=2
BD=2![]() ,于是得到A点坐标为(2,2
,于是得到A点坐标为(2,2![]() );
);
当点C在第四象限,如图2,作AD⊥BC于D,同理可得BD=CD=![]() BC=2,AD=
BC=2,AD=![]() BD=2
BD=2![]() ,则A点坐标为(2,﹣2
,则A点坐标为(2,﹣2![]() ).
).
解:当点C在第一象限,如图1,

作AD⊥BC于D,
∵等边三角形ABC的边长为4,
∴BD=CD=![]() BC=2,∠BAD=30°,
BC=2,∠BAD=30°,
∴AD=![]() BD=2
BD=2![]() ,
,
∴A点坐标为(2,2![]() );
);
当点C在第四象限,如图2,

作AD⊥BC于D,同理可得BD=CD=![]() BC=2,AD=
BC=2,AD=![]() BD=2
BD=2![]() ,
,
∴A点坐标为(2,﹣2![]() ),
),
综上所述,点A的坐标为(2,2![]() )或(2,﹣2
)或(2,﹣2![]() ).
).
故答案为(2,2![]() )或(2,﹣2
)或(2,﹣2![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】张家界到长沙的距离约为320km,小明开着大货车,小华开着小轿车,都从张家界同时去长沙,已知小轿车的速度是大货车的1.25倍,小华比小明提前1小时到达长沙.试问:大货车和小轿车的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是⊙O上一点,OA⊥AB,且OA=1,AB=
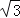 ,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.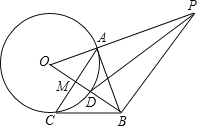
(1)求证:BC是⊙O的切线;
(2)过点B作BP⊥OB,交OA的延长线于点P,连接PD,求sin∠BPD的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
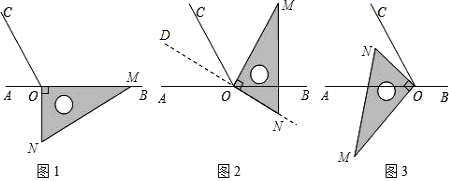
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 (直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两城市之间有动车组高速列车,也有普通快车,如图所示,OA是一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运动时间t(h)的函数图象,请根据图中信息,解答下列问题:
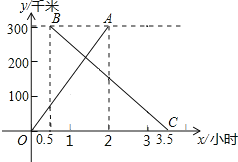
(1)点B的横坐标0.5的实际意义是 ,点B的纵坐标300的实际意义是 ;
(2)求OA与BC所在直线的函数表达式;
(3)求动车组列车出发后多长时间与普通列车相遇.
-
科目: 来源: 题型:
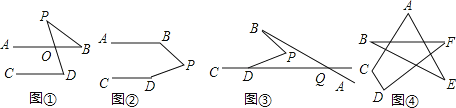
查看答案和解析>>【题目】如图①,若AB∥CD,点P在AB,CD外部,则有∠D=∠BOD,又因为∠BOD是△POB的外角,故∠BOD=∠BPD+∠B,得∠BPD=∠D﹣∠B.
探究一:将点P移到AB,CD内部,如图②,则∠BPD,∠B,∠D之间有何数量关系?并证明你的结论;
探究二:在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD延长线于点Q,如图③,则∠BPD,∠B,∠PDQ,∠BQD之间又有何数量关系?并证明你的结论;
探究三:在图④中,直接根据探究二的结论,写出∠A+∠B+∠C+∠D+∠E+∠F的度数.
相关试题

