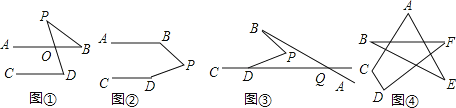
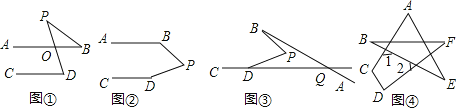
【题目】如图①,若AB∥CD,点P在AB,CD外部,则有∠D=∠BOD,又因为∠BOD是△POB的外角,故∠BOD=∠BPD+∠B,得∠BPD=∠D﹣∠B.
探究一:将点P移到AB,CD内部,如图②,则∠BPD,∠B,∠D之间有何数量关系?并证明你的结论;
探究二:在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD延长线于点Q,如图③,则∠BPD,∠B,∠PDQ,∠BQD之间又有何数量关系?并证明你的结论;
探究三:在图④中,直接根据探究二的结论,写出∠A+∠B+∠C+∠D+∠E+∠F的度数.
参考答案:
【答案】探究一:∠B+∠BPD+∠D=360°;探究二:∠BPD=∠B+∠PDQ+∠BQD;探究三:360°.
【解析】
试题分析:探究一,过点P作PE∥AB,根据平行线的性质可知∠B+∠BPE=180°,∠D+∠EPD=180°,即∠B+∠BPD+∠D=360°.
探究二,连接QP并延长至E,根据∠BPE是△BPQ的一个外角,得到∠BPE=∠BQP+∠B.同理得到∠EPD=∠DQP+∠PDQ,从而∠BPD=∠B+∠PDQ+∠BQD.
探究三,根据三角形外角性质和四边形的内角和等于360°得出即可.
探究一,∠B+∠BPD+∠D=360°,
证明:过点P作PE∥AB,如图②,
∴∠B+∠BPE=180°,
又∵AB∥CD,
∴PE∥CD,
∴∠D+∠EPD=180°,
∴∠B+∠BPE+∠D+∠EPD=360°,
即∠B+∠BPD+∠D=360°;
探究二,∠BPD=∠B+∠PDQ+∠BQD,
证明:连接QP并延长至E,如图③,
∵∠BPE是△BPQ的一个外角,
∴∠BPE=∠BQP+∠B.
同理:∠EPD=∠DQP+∠PDQ.
∴∠BPE+∠EPD=∠BQP+∠B+∠DQP+∠PDQ.
即:∠BPD=∠B+∠PDQ+∠BQD;
探究三,如图④,∵∠1=∠A+∠E,∠2=∠B+∠F,∠1+∠2+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于边长为4的等边三角形ABC,以点B为坐标原点,底边BC方向所在的直线为x轴正方向,建立平面直角坐标系,则顶点A的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
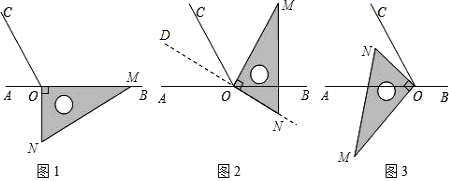
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 (直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两城市之间有动车组高速列车,也有普通快车,如图所示,OA是一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运动时间t(h)的函数图象,请根据图中信息,解答下列问题:
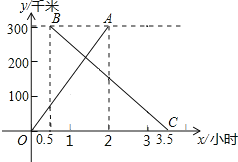
(1)点B的横坐标0.5的实际意义是 ,点B的纵坐标300的实际意义是 ;
(2)求OA与BC所在直线的函数表达式;
(3)求动车组列车出发后多长时间与普通列车相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
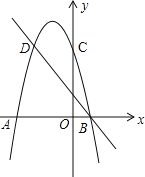
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某企业向雅安地震灾区捐助价值26万元的甲、乙两种帐篷共300顶.已知甲种帐篷每顶800元,乙种帐篷每顶1000元,问甲、乙两种帐篷各多少顶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
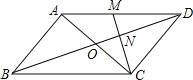
(1)求BD的长;
(2)在直线AC的同侧,以点O为位似中心,作出△CON的位似三角形,并使△CON与和它位似的三角形的位似比是1:2.(写出结果,不写作法,保留作图痕迹).
相关试题

