【题目】如图,点A是⊙O上一点,OA⊥AB,且OA=1,AB=![]() ,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
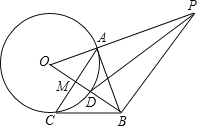
(1)求证:BC是⊙O的切线;
(2)过点B作BP⊥OB,交OA的延长线于点P,连接PD,求sin∠BPD的值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)连结OC,根据垂径定理由AC⊥OB得AM=CM,于是可判断OB为线段AC的垂直平分线,所以BA=BC,然后利用“SSS”证明△OAB≌△OCB,得到∠OAB=∠OCB,由于∠OAB=90°,则∠OCB=90°,于是可根据切线的判定定理得BC是⊙O的切线;
(2)在Rt△OAB中,根据勾股定理计算出OB=2,根据含30度的直角三角形三边的关系得∠ABO=30°,∠AOB=60°,在Rt△PBO中,由∠BPO=30°得到PB=![]() OB=2
OB=2![]() ;在Rt△PBD中,BD=OB﹣OD=1,根据勾股定理计算出PD=
;在Rt△PBD中,BD=OB﹣OD=1,根据勾股定理计算出PD=![]() ,然后利用正弦的定义求sin∠BPD的值.
,然后利用正弦的定义求sin∠BPD的值.
(1)证明:连结OC,如图,
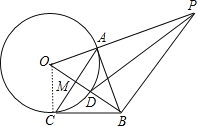
∵AC⊥OB,
∴AM=CM,
∴OB为线段AC的垂直平分线,
∴BA=BC,
在△OAB和△OCB中
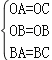 ,
,
∴△OAB≌△OCB(SSS),
∴∠OAB=∠OCB,
∵OA⊥AB,
∴∠OAB=90°,
∴∠OCB=90°,
∴OC⊥BC,
故BC是⊙O的切线;
(2)解:在Rt△OAB中,OA=1,AB=![]() ,
,
∴OB=![]() =2,
=2,
∴∠ABO=30°,∠AOB=60°,
∵PB⊥OB,
∴∠PBO=90°,∠BPO=30°,
在Rt△PBO中,OB=2,
∴PB=![]() OB=2
OB=2![]() ,
,
在Rt△PBD中,BD=OB﹣OD=2﹣1=1,PB=2![]() ,
,
∴PD=![]() =
=![]() ,
,
∴sin∠BPD=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a、b、c是△ABC的三边,满足(b﹣3)2+|c﹣4|=0,a为奇数,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张家界到长沙的距离约为320km,小明开着大货车,小华开着小轿车,都从张家界同时去长沙,已知小轿车的速度是大货车的1.25倍,小华比小明提前1小时到达长沙.试问:大货车和小轿车的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于边长为4的等边三角形ABC,以点B为坐标原点,底边BC方向所在的直线为x轴正方向,建立平面直角坐标系,则顶点A的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
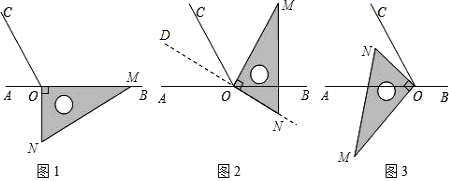
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 (直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两城市之间有动车组高速列车,也有普通快车,如图所示,OA是一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运动时间t(h)的函数图象,请根据图中信息,解答下列问题:
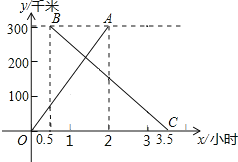
(1)点B的横坐标0.5的实际意义是 ,点B的纵坐标300的实际意义是 ;
(2)求OA与BC所在直线的函数表达式;
(3)求动车组列车出发后多长时间与普通列车相遇.
相关试题

