【题目】如图,已知A,B两点的坐标分别为A![]() ,B(2,0),直线AB与反比例函数
,B(2,0),直线AB与反比例函数![]() 的图像交与点C和点D(-1,a).
的图像交与点C和点D(-1,a).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数;
(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.

参考答案:
【答案】(1)![]() ,
, ![]() ;(2)∠ACO =30°;(3)AB'= 2.
;(2)∠ACO =30°;(3)AB'= 2.
【解析】试题分析:(1)设直线AB的解析式为![]() ,
,
将A(0,2![]() ),B(2,0)代入解析式
),B(2,0)代入解析式![]() 中,得
中,得
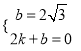 ,解得
,解得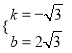 。
。
∴直线AB的解析式为![]() 。
。

将D(-1, ![]() )代入
)代入![]() 得,
得, ![]() 。
。
∴点D坐标为(-1, ![]() )。
)。
将D(-1, ![]() )代入
)代入![]() 中得,
中得, ![]() 。
。
∴反比例函数的解析式为![]() 。
。
(2)解方程组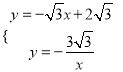 得
得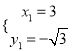 ,
, 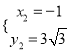 。
。
∴点C坐标为(3, ![]() ),
),
过点C作CM⊥![]() 轴于点M,则在Rt△OMC中,
轴于点M,则在Rt△OMC中,
![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() 。
。
在Rt△AOB中, ![]() =
=![]() ,∴
,∴![]() 。
。
∴∠ACO=![]() 。
。
(3)如图,∵OC′⊥AB,∠ACO=30°,

∴![]() = ∠COC′=90°-30°=60°,∠BOB′=
= ∠COC′=90°-30°=60°,∠BOB′= ![]() =60°。
=60°。
∴∠AOB′=90°-∠BOB′=30°。
∵∠OAB=90°-∠ABO=30°,∴∠AOB′=∠OAB,
∴AB′= OB′=2.
答:当α为60度时OC′⊥AB,此时线段AB′的长为2。
-
科目: 来源: 题型:
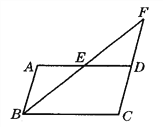
查看答案和解析>>【题目】如图,平行四边形ABCD中,点E是AD的中点,BE的延长线与CD的延长线交于点F.
(1)求证:△ABE≌△DFE;
(2)试连结BD,AF,判断四边形ABDF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如右图所示,直线y1=-2x+3和直线y2=mx-1分别交y轴于点A,B,两直线交于点C(1,n).
(1)求m,n的值;
(2)求ΔABC的面积;
(3)请根据图象直接写出:当y1<y2时,自变量的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x﹣6与反比例函数
 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
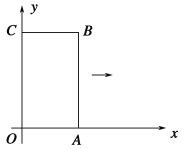
查看答案和解析>>【题目】如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为________(用含n的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】六年级(1)班从学校出发,乘大巴车去农场进行实践活动,之后返回学校(大巴车行驶速度不变),下图反映的是大巴车行驶路程与时间之间的关系。请同学们观察图象,进行数据分析,求大巴车离开学校多少小时时,大巴车与农场相距
 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
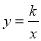 (k<0)的图像经过点A(
(k<0)的图像经过点A(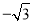 ,m),过点A作AB⊥x轴于点,且△AOB的面积为
,m),过点A作AB⊥x轴于点,且△AOB的面积为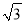 .
.(1)求k和m的值;
(2)若一次函数y=ax+1的图像经过点A,并且与x轴相交于点C,求∠ACO的度数及
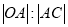 的值.
的值.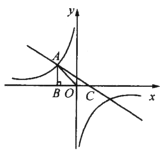
相关试题

