Question

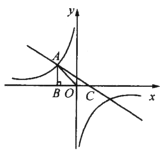
【题目】如图，已知反比例函数（k<0）的图像经过点A（，m），过点A作AB⊥x轴于点，且△AOB的面积为．

（1）求k和m的值；

（2）若一次函数y=ax+1的图像经过点A，并且与x轴相交于点C，求∠ACO的度数及的值．

Answer 1

【答案】（1）k=；（2）│AO│：│AC│= ．

【解析】试题分析：（1）根据的面积为，得到反比例函数的解析式，进而可以求出的值．
（2）把A代入y=ax+1中，就可以求出的值，得到函数的解析式，因而求出 点的坐标，在中就可以求出的值，得到的值，在中，根据勾股定理就可以求出的值．

试题解析：

（1）∵，

∴，∴m=2，

又过点A，则，

∴k=．

（2）∵直线y=ax+1过A，

∴，

∴．

当y=0时， ，

∴C，BC=，

又tan∠ACO=，

∴∠ACO=30°．在Rt△ABO中，AO=，在Rt△ABC中，AC=2AB=4．

∴│AO│：│AC│=．