【题目】六年级(1)班从学校出发,乘大巴车去农场进行实践活动,之后返回学校(大巴车行驶速度不变),下图反映的是大巴车行驶路程与时间之间的关系。请同学们观察图象,进行数据分析,求大巴车离开学校多少小时时,大巴车与农场相距![]() 。
。

参考答案:
【答案】大巴车离开学校后![]() 小时或
小时或![]() 小时时与农场相距
小时时与农场相距![]() .
.
【解析】
图中反应的行驶的路程和时间的关系,有图可知,0~1小时之间时,大巴车出发去农场,1~3小时之间,大巴车已经到了农场未动,此时正在参与实践过程,3~4小时之间,大巴车出发返回学校.所以大巴车与农场相距![]() 的时刻有两处,分别是出发去农场时和返程回学校时.
的时刻有两处,分别是出发去农场时和返程回学校时.
由图象可知:出发1小时,对应着大巴车已到了农场,学校与农场相距![]() ,所以大巴车的速度为40千米/小时,往返过程中都存在大巴车与农场相距10千米的情况。
,所以大巴车的速度为40千米/小时,往返过程中都存在大巴车与农场相距10千米的情况。
去时:大巴车离开学校行驶30km时,距离农场10km.
则用时为30÷40=![]() 小时
小时
返回时:大巴车只要行驶10km时,距离农场10km.
则用时为10÷40=![]() 小时,又因为题中问的是大巴车离开学校多少小时时,距离农场10km
小时,又因为题中问的是大巴车离开学校多少小时时,距离农场10km
所以用时为![]() +3=
+3=![]() 小时
小时
故答案为:大巴车离开学校后![]() 小时或
小时或![]() 小时时与农场相距
小时时与农场相距![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x﹣6与反比例函数
 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B两点的坐标分别为A
 ,B(2,0),直线AB与反比例函数
,B(2,0),直线AB与反比例函数 的图像交与点C和点D(-1,a).
的图像交与点C和点D(-1,a).(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数;
(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.

-
科目: 来源: 题型:
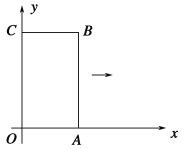
查看答案和解析>>【题目】如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为________(用含n的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
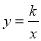 (k<0)的图像经过点A(
(k<0)的图像经过点A(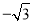 ,m),过点A作AB⊥x轴于点,且△AOB的面积为
,m),过点A作AB⊥x轴于点,且△AOB的面积为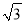 .
.(1)求k和m的值;
(2)若一次函数y=ax+1的图像经过点A,并且与x轴相交于点C,求∠ACO的度数及
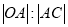 的值.
的值.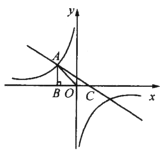
-
科目: 来源: 题型:
查看答案和解析>>【题目】惠农种子公司以一定价格销售“丰收一号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间函数关系如图所示.下列四种说法:①一次购买30千克种子时,付款金额为1 000元;②一次购买种子数量不超过10千克时,销售价格为50元/千克;③一次购买10千克以上种子时,超过10千克的那部分种子的价格打五折;④一次购买40千克种子比分两次购买且每次购买20千克种子少花200元钱,其中正确的个数是( )
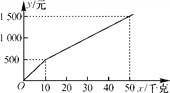
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=10,AC=2
 ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
 =8,CD=
=8,CD= =2,
=2,此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
 =8,CD=
=8,CD= =2,
=2,此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
相关试题

