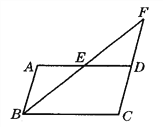
【题目】如图,平行四边形ABCD中,点E是AD的中点,BE的延长线与CD的延长线交于点F.
(1)求证:△ABE≌△DFE;
(2)试连结BD,AF,判断四边形ABDF的形状,并证明你的结论.
参考答案:
【答案】(1)证明见试题解析;(2)平行四边形,理由见试题解析.
【解析】
(1)用ASA证明△ABE≌△DFE;
(2)四边形ABDF是平行四边形,可用一组对边平行且相等的四边形是平行四边形来证明.
(1)∵四边形ABCD是平行四边形,
∴AB//CF,
∴∠1=∠2,∠3=∠4,
∵E是AD的中点,
∴AE=DE,
∴△ABE≌△DFE;
(2)四边形ABDF是平行四边形.理由如下:
∵△ABE≌△DFE,
∴AB=DF,
又∵AB//DF,
∴四边形ABDF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查学生对“节约教育”内容的了解程度(程度分为:“
 —了解很多”,“
—了解很多”,“ —了解较多”,“
—了解较多”,“ —了解较少”,“
—了解较少”,“ —不了解”),对某中学的部分学生进行了调查,将这次调查的结果绘制成以下两幅统计图.根据以上信息,解答下列问顾:
—不了解”),对某中学的部分学生进行了调查,将这次调查的结果绘制成以下两幅统计图.根据以上信息,解答下列问顾: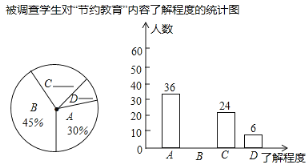
(1)本次调查了多少名学生?
(2)若该校共有1800名学生,请你估计这所学校的所有学生中,对“节约教育”内容“了解较多”的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )
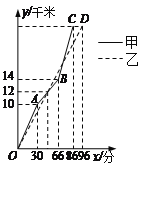
A.甲先到达终点
B.前30分钟,甲在乙的前面
C.第48分钟时,两人第一次相遇
D.这次比赛的全程是28千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的曲线是函数y=
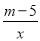 (m为常数)图象的一支.
(m为常数)图象的一支.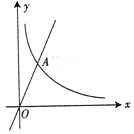
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例
函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如右图所示,直线y1=-2x+3和直线y2=mx-1分别交y轴于点A,B,两直线交于点C(1,n).
(1)求m,n的值;
(2)求ΔABC的面积;
(3)请根据图象直接写出:当y1<y2时,自变量的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x﹣6与反比例函数
 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B两点的坐标分别为A
 ,B(2,0),直线AB与反比例函数
,B(2,0),直线AB与反比例函数 的图像交与点C和点D(-1,a).
的图像交与点C和点D(-1,a).(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数;
(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.

相关试题

