【题目】如右图所示,直线y1=-2x+3和直线y2=mx-1分别交y轴于点A,B,两直线交于点C(1,n).
(1)求m,n的值;
(2)求ΔABC的面积;
(3)请根据图象直接写出:当y1<y2时,自变量的取值范围.

参考答案:
【答案】(1)n=1,m=2;(2)2;(3)当y1<y2时,x>1.
【解析】
(1)利用待定系数法把![]() 点坐标代入
点坐标代入![]() 可算出
可算出![]() 的值,然后再把
的值,然后再把![]() 点坐标代入
点坐标代入![]() 可算出
可算出![]() 的值;
的值;
(2)首先根据函数解析式计算出![]() 两点坐标,然后再根据
两点坐标,然后再根据![]() 三点坐标求出
三点坐标求出![]() 的面积;
的面积;
(3)根据![]() 点坐标,结合一次函数与不等式的关系可得出答案.
点坐标,结合一次函数与不等式的关系可得出答案.
解:(1)∵点C(1,n)在直线y1=-2x+3上,∴n=-2×1+3=1,∴C(1,1),∵y2=mx-1过点C(1,1),∴1=m-1,解得m=2. (2)当x=0时,y1=-2x+3=3,则A(0,3),当x=0时,y2=2x-1=-1,则B(0,-1),∴ΔABC的面积为![]() ×4×1=2.
×4×1=2.
(3)∵C(1,1),∴当y1<y2时,x>1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市劲威乡A、B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C、D两处的费用分别为每吨15元和18元.设从A村运往C仓库的柑橘重量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元和yB元.
【1】请填写下表

【2】求出yA、yB与x之间的函数解析式;
【3】试讨论A、B两村中,哪个村的运费最少;
【4】考虑B村的经济承受能力,B村的柑橘运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?求出这个最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
①0是绝对值最小的有理数;②相反数大于本身的数是负数;③数轴上原点两侧的数互为相反数;
 是有理数.
是有理数.A. ①② B. ①③ C. ①②③ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=
 (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.
方案一:每千克种子价格为4元,均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.
(1)请分别求出方案一、方案二中购买的种子数量x(千克)与付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组线段中,可以组成直角三角形的是( )
A. 4,5,6 B. 3,4,5 C. 5,6,7 D. 1,
 ,3
,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(
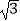 ,1)在反比例函数y=
,1)在反比例函数y= 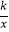 的图象上.
的图象上. 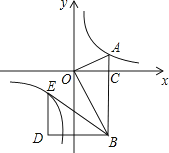
(1)求反比例函数y=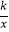 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP= S△AOB , 求点P的坐标;
S△AOB , 求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
相关试题

