【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ,与x轴交于A、B两点(点A在点B的左侧).
,与x轴交于A、B两点(点A在点B的左侧).
(1)求点A和点B的坐标;
(2)若点P(m,n)是抛物线上的一点,过点P作x轴的垂线,垂足为点D.
①在![]() 的条件下,当
的条件下,当![]() 时,n的取值范围是
时,n的取值范围是![]() ,求抛物线的表达式;
,求抛物线的表达式;
②若D点坐标(4,0),当![]() 时,求a的取值范围.
时,求a的取值范围.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】(1)令y=0,可得![]() ,解方程可得A,B两点坐标;(2)①抛物线的对称轴为直线:
,解方程可得A,B两点坐标;(2)①抛物线的对称轴为直线:![]() ; 由题意二次函数的顶点为
; 由题意二次函数的顶点为![]() ,再代入解析式可求a. ②由D点坐标(4,0),
,再代入解析式可求a. ②由D点坐标(4,0),![]() ,又因点P的横坐标为4,代入解析式得
,又因点P的横坐标为4,代入解析式得![]() =PD,由
=PD,由![]() ,可推出a的取值范围.
,可推出a的取值范围.
(1)把![]() 代入二次函数得:
代入二次函数得:![]() 即
即![]()
∴![]()
∵点A在点B的左侧,
∴![]() ,
,![]()
(2)①抛物线的对称轴为直线:![]() ;
;
由题意二次函数的顶点为![]() ,
,
代入解析式,可得![]()
抛物线的解析式为![]()
②∵D点坐标(4,0),![]()
∴点P的横坐标为4,代入![]() 得
得![]()
∵D点坐标(4,0),A点坐标(![]() ,0)
,0)
∴![]()
∵![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
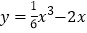 的图象与性质.小彤根据学习函数的经验,对函数
的图象与性质.小彤根据学习函数的经验,对函数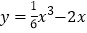 的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:x
-4
-3.5
-3
-2
-1
0
1
2
3
3.5
4
y
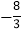
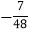


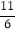
0
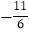
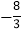
m
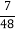

(1)求m的值为 ;
(2)如图,在平面直角坐标系x0y 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(3)方程
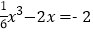 实数根的个数为 ;
实数根的个数为 ; (4)观察图象,写出该函数的一条性质 ;
(5)在第(2)问的平面直角坐标系中画出直线
 ,根据图象写出方程
,根据图象写出方程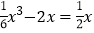 的一个正数根约为 (精确到0.1).
的一个正数根约为 (精确到0.1).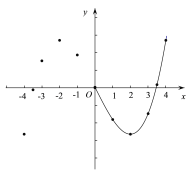
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(0,a),点B(b,0),其中a,b满足
 =0,点C(m,n)在第一象限,已知
=0,点C(m,n)在第一象限,已知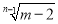 是2的立方根.
是2的立方根.
(1)直接写出A,B,C三点的坐标;
(2)求出△ABC的面积;
(3)如图2,延长BC交y轴于D点,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,BE=CE,下面四个结论:①BP=CP;②AD⊥BC;③AE平分∠BAC;④∠PBC=∠PCB.其中正确的结论个数有( )个.
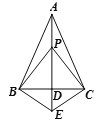
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
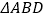 与
与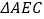 都是等边三角形,
都是等边三角形,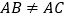 ,下列结论中,正确的个数是( )①
,下列结论中,正确的个数是( )①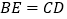 ;②
;②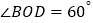 ;③
;③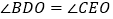 ;④若
;④若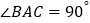 ,且
,且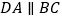 ,则
,则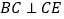 .
.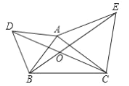
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形 对.
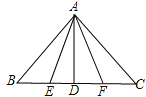
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
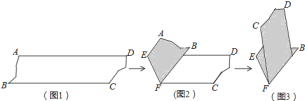
A.120°B.108°C.126°D.114°
相关试题

