【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
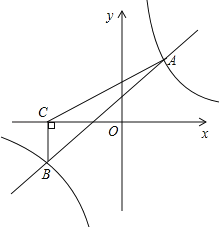
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b≥![]() 的解集 ;
的解集 ;
(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
参考答案:
【答案】(1)y=![]() ,y=x+1;(2)x>2或﹣3<x<0.(3)5.
,y=x+1;(2)x>2或﹣3<x<0.(3)5.
【解析】
试题分析:(1)把A\的坐标代入反比例函数的解析式,即可求出反比例函数的解析式,求出B的坐标,把A、B的坐标代入一次函数的解析式,即可求出一次函数的解析式;
(2)根据A、B的 坐标结合图象得出即可.
(3)设AB与x轴交点为D,根据一次函数的解析式即可求得D的坐标,根据S△ABC=S△ACD+S△BDC就可求得三角形的面积.
解:(1)从图象可知A的坐标是(2,3),B的坐标是(﹣3,n),
把A的坐标代入反比例函数的解析式得:k=6,
即反比例函数的解析式是y=![]() ,
,
把B的坐标代入反比例函数的解析式得:n=﹣2,
即B的坐标是(﹣3,﹣2),
把A、B的坐标代入一次函数的解析式得:
![]() ,
,
解得:k=1,b=1.
即一次函数的解析式是y=x+1;
(2)∵由图象可知使一次函数的值大于反比例函数的值的x取值范围是x>2或﹣3<x<0.
∴不等式kx+b≥![]() 的解集为x>2或﹣3<x<0.
的解集为x>2或﹣3<x<0.
(3)设AB与x轴交点为D,则D(﹣1,0),
则S△ABC=S△ACD+S△BDC=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m=( )
A. 2 B. -2 C. 4 D. -4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系
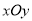 (如图)中,抛物线
(如图)中,抛物线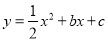 经过点
经过点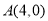 、点
、点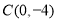 ,点
,点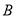 与点
与点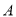 关于这条抛物线的对称轴对称;
关于这条抛物线的对称轴对称;
(1)求配方法求这条抛物线的顶点坐标;
(2)联结
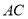 、
、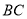 ,求
,求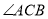 的正弦值;
的正弦值;(3)点
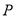 是这条抛物线上的一个动点,设点
是这条抛物线上的一个动点,设点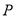 的横坐标为
的横坐标为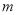 (
(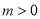 ),过点
),过点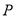 作
作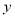 轴的垂线
轴的垂线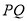 ,垂足为
,垂足为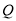 ,如果
,如果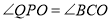 ,求
,求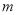 的值;
的值; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )

A.2cm B.5cm C.6cm D.7cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C.
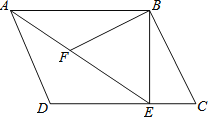
(1)求证:△ABF∽△EAD;
(2)若BC=4,AB=3
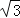 ,BE=3,求BF的长.
,BE=3,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小军用50元钱买单价为8元的笔记本,他剩余的钱数Q(元)与他买这种笔记本的本数x之间的关系式为Q=50-8x,则下列说法正确的是( )
A. Q和x是变量 B. Q是自变量 C. 50和x是常量 D. x是Q的函数
-
科目: 来源: 题型:
查看答案和解析>>【题目】实数与数轴上的点是______的关系.
相关试题

