【题目】已知在平面直角坐标系![]() (如图)中,抛物线
(如图)中,抛物线![]() 经过点
经过点![]() 、点
、点![]() ,点
,点![]() 与点
与点![]() 关于这条抛物线的对称轴对称;
关于这条抛物线的对称轴对称;

(1)求配方法求这条抛物线的顶点坐标;
(2)联结![]() 、
、![]() ,求
,求![]() 的正弦值;
的正弦值;
(3)点![]() 是这条抛物线上的一个动点,设点
是这条抛物线上的一个动点,设点![]() 的横坐标为
的横坐标为![]() (
(![]() ),过点
),过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,如果
,如果![]() ,求
,求![]() 的值;
的值;
参考答案:
【答案】(1)定点坐标(1,-![]() );(2)
);(2)![]() ;(3)
;(3)![]() 或
或![]() (舍去负
(舍去负
【解析】
试题分析:(1)因A、C在抛物线![]() 上,代入可把抛物线y的解析式求出,通过配方即可得抛物线的顶点坐标.
上,代入可把抛物线y的解析式求出,通过配方即可得抛物线的顶点坐标.
(2)由(1)可知对称轴x=1,且A、B关于x=1对称,可知B(-2,0),AB=6.
又因△ABH为等腰三角形,根据![]() ,所以
,所以![]() ,在Rt△BOC中,BC=
,在Rt△BOC中,BC=![]() ,又因在Rt△BCH中,可求出
,又因在Rt△BCH中,可求出![]() .
.
(3)要求P的横坐标M,就要知道P点构成的Rt△OPQ中的![]() 的值,又因
的值,又因![]() ,故
,故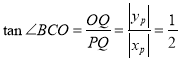 ,在设P
,在设P![]() ,代入抛物线
,代入抛物线![]() ,解得
,解得![]() 或
或![]() (舍去负值).
(舍去负值).
试题解析:(1)代入A(4,0),C(0,-4),得抛物线解析式为![]() ,配方得
,配方得![]() ,
,![]() 顶点坐标为(1,
顶点坐标为(1,![]() ).
).
作![]() 于H,由已知,抛物线对称轴为直线x=1,故B(-2,0),AB=6,由OA=OC=4,则
于H,由已知,抛物线对称轴为直线x=1,故B(-2,0),AB=6,由OA=OC=4,则![]() ,故△ABH为等腰直角三角形.因此BH=AH=
,故△ABH为等腰直角三角形.因此BH=AH=![]() ,又
,又![]() ,故Rt△BCO中,
,故Rt△BCO中,![]() .
.
(3)Rt△BCO中,![]() ,故Rt△OPQ中,
,故Rt△OPQ中, ,故可设
,故可设![]() ,分别代入抛物线解析式
,分别代入抛物线解析式![]() ,解得
,解得![]() 或
或![]() (舍去负值).
(舍去负值).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件工艺品进价为100元,标价135元售出,每天可售出100件.根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价的钱数为( )
A.5元 B.10元 C.0元 D.36元
-
科目: 来源: 题型:
查看答案和解析>>【题目】把直线y=-x-1沿x轴向右平移2个单位长度,所得直线对应的函数表达式为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m=( )
A. 2 B. -2 C. 4 D. -4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )

A.2cm B.5cm C.6cm D.7cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.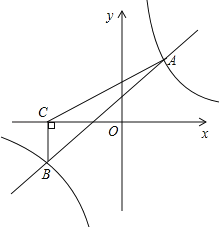
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b≥
 的解集 ;
的解集 ;(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C.
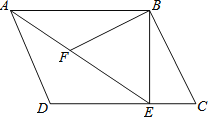
(1)求证:△ABF∽△EAD;
(2)若BC=4,AB=3
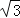 ,BE=3,求BF的长.
,BE=3,求BF的长.
相关试题

