【题目】如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C.
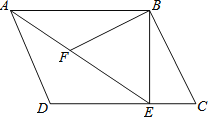
(1)求证:△ABF∽△EAD;
(2)若BC=4,AB=3![]() ,BE=3,求BF的长.
,BE=3,求BF的长.
参考答案:
【答案】(1)见解析;(2)2![]() .
.
【解析】
试题分析:(1)可通过证明∠BAF=∠AED,∠AFB=∠D,证得△ABF∽△EAD;
(2)根据(1)的相似三角形可得出关于AB,AE,AD,BF的比例关系,有了AD,AB的长,只需求出AE的长即可.可在直角三角形ABE中用勾股定理求出AE的长,这样就能求出BF的长了.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠BAF=∠AED,∠D+∠C=180°,
∵∠AFB+∠BFE=180°,∠BFE=∠C,
∴∠AFB+∠C=180°,
∴∠D=∠AFB,
∴△ABF∽△EAD;
(2)解:∵AB∥CD,BE⊥CD,
∴∠ABE=90°
∵AB=3![]() ,BE=3,
,BE=3,
∴在Rt△ABE中,AE=![]() =
=![]() =6,
=6,
∵△ABF∽△EAD,
∴![]() ,
,
∴BF=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系
 (如图)中,抛物线
(如图)中,抛物线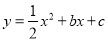 经过点
经过点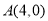 、点
、点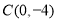 ,点
,点 与点
与点 关于这条抛物线的对称轴对称;
关于这条抛物线的对称轴对称;
(1)求配方法求这条抛物线的顶点坐标;
(2)联结
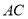 、
、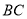 ,求
,求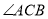 的正弦值;
的正弦值;(3)点
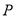 是这条抛物线上的一个动点,设点
是这条抛物线上的一个动点,设点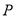 的横坐标为
的横坐标为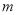 (
(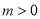 ),过点
),过点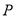 作
作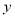 轴的垂线
轴的垂线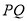 ,垂足为
,垂足为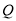 ,如果
,如果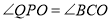 ,求
,求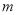 的值;
的值; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )

A.2cm B.5cm C.6cm D.7cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.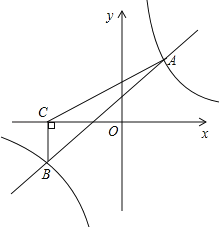
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b≥
 的解集 ;
的解集 ;(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军用50元钱买单价为8元的笔记本,他剩余的钱数Q(元)与他买这种笔记本的本数x之间的关系式为Q=50-8x,则下列说法正确的是( )
A. Q和x是变量 B. Q是自变量 C. 50和x是常量 D. x是Q的函数
-
科目: 来源: 题型:
查看答案和解析>>【题目】实数与数轴上的点是______的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形的一边长是14,下列各组数中能分别作为它的两条对角线的是( )
A、10与16 B、12与16 C、20与22 D、10与40
相关试题

