【题目】如图,在等边△ABC中,点F是AC边上一点,延长BC到点D,使BF=DF,若CD=CF,求证: 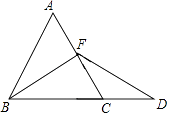
(1)点F为AC的中点;
(2)过点F作FE⊥BD,垂足为点E,请画出图形并证明BD=6CE.
参考答案:
【答案】
(1)解:∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵CF=CD,
∴∠CFD=∠D,
∴∠ACB=2∠D,即∠D= ![]() ∠ACB=30°,
∠ACB=30°,
∵FB=FD,
∴∠FBD=∠D=30°,
∴BF平分∠ABC,
∴AF=CF,即点F为AC的中点
(2)解:如图,
在Rt△EFC中,CF=2CE,
而CD=CF,
∴CF=2CE,
在Rt△BCF中,BC=2CF,
∴BC=4CE,
∴BD=6CE.
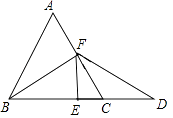
【解析】(1)根据等边三角形的性质得∠ABC=∠ACB=60°,利用∠CFD=∠D,则根据三角形外角性质得到∠ACB=2∠D,即∠D= ![]() ∠ACB=30°,然后利用FB=FD得到∠FBD=∠D=30°,则BF平分∠ABC,于是根据等边三角形的性质可得到点F为AC的中点;(2)如图,过点F作FE⊥BD于E,利用含30度的直角三角形三边的关系得到CF=2CE,而CD=CF,则CF=2CE,再利用BC=2CF,所以BD=6CE.
∠ACB=30°,然后利用FB=FD得到∠FBD=∠D=30°,则BF平分∠ABC,于是根据等边三角形的性质可得到点F为AC的中点;(2)如图,过点F作FE⊥BD于E,利用含30度的直角三角形三边的关系得到CF=2CE,而CD=CF,则CF=2CE,再利用BC=2CF,所以BD=6CE.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车经销商购进
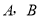 两种型号的低排量汽车,其中
两种型号的低排量汽车,其中 型汽车的进货单价比
型汽车的进货单价比 型汽车的进货单价多2万元,经销商花50万元购进
型汽车的进货单价多2万元,经销商花50万元购进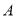 型汽车的数量与花40万元购进
型汽车的数量与花40万元购进 型汽车的数量相等.销售中发现
型汽车的数量相等.销售中发现 型汽车的每周销量
型汽车的每周销量 (台)与售价
(台)与售价 (万元/台)满足函数关系式
(万元/台)满足函数关系式 ,
,  型汽车的每周销量
型汽车的每周销量 (台)与售价
(台)与售价 (万元/台)满足函数关系式
(万元/台)满足函数关系式 .
.(1)求
 两种型号的汽车的进货单价;
两种型号的汽车的进货单价;(2)已知
 型汽车的售价比
型汽车的售价比 型汽车的售价高2万元/台,设
型汽车的售价高2万元/台,设 型汽车售价为
型汽车售价为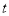 万元/台.每周销售这两种车的总利润为
万元/台.每周销售这两种车的总利润为 万元,求
万元,求 与
与 的函数关系式,
的函数关系式,  两种型号的汽车售价各为多少时,每周销售这两种车的总利润最大?最大总利润是多少万元?
两种型号的汽车售价各为多少时,每周销售这两种车的总利润最大?最大总利润是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在
 中,
中,  ,
, ,延长
,延长 到
到 ,使
,使 ,以
,以 为圆心,
为圆心,  长为半径作⊙
长为半径作⊙ 交
交 延长线于点
延长线于点 ,连接
,连接 .
.(1)求证:
 是⊙
是⊙ 的切线;
的切线;(2)若
 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个圆柱的三种视图,小明同学求出其中两种视图的面积分别为6和10,则该圆柱第三种视图的面积为( )
A.6B.10C.4D.6或10
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个相似三角形的对应边之比为1:3,则它们的周长比为( )
A. 1:9 B. 9:1 C. 1:6 D. 1:3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.

(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一点,连接PA、PB、PO,
①若△POA的面积是△POB面积的
 倍.求点P的坐标;
倍.求点P的坐标;②当四边形AOBP的面积最大时,求点P的坐标;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.

相关试题

