【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角
的一个角![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
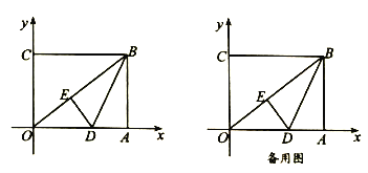
(1)线段![]() 的长度为__________;
的长度为__________;
(2)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)15;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据勾股定理即可解决问题;
(2)设AD=x,则OD=OA=AD=12-x,根据轴对称的性质,DE=x,BE=AB=9,又OB=15,可得OE=OB-BE=15-9=6,在Rt△OED中,根据OE2+DE2=OD2,构建方程即可解决问题;
(3)过点E作EP∥BD交BC于点P,过点P作PQ∥DE交BD于点Q,则四边形DEPQ是平行四边形,再过点E作EF⊥OD于点F,想办法求出最小PE的解析式即可解决问题。
解:(1)在Rt△ABC中,∵OA=12,AB=9,
![]()
故答案为15.
(2)如图,
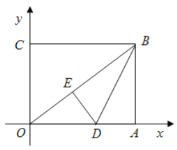
设![]() ,则
,则![]()
根据轴对称的性质,![]() ,
,
又![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]()
设直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]()
则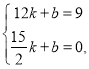 ,
,
解得![]()
∴直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]() .
.
故答案为:![]()
(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是平行四边形,再过点
是平行四边形,再过点![]() 作
作![]() 于点
于点![]() ,
,
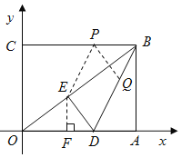
由![]()
得![]() ,即点
,即点![]() 的纵坐标为
的纵坐标为![]() ,
,
又点![]() 在直线
在直线![]() :
:![]() 上,
上,
∴![]() ,解得
,解得![]() ,
,
![]()
由于![]() ,所以可设直线
,所以可设直线![]() ,
,
∵![]() 在直线
在直线![]() 上
上
∴![]() ,解得
,解得![]()
∴直线![]() 为
为![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,完成(1)、(2)小题.在平面直角坐标系中,已知
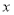 轴上两点
轴上两点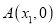 ,
,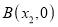 的距离记作
的距离记作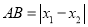 ,如果
,如果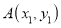 ,
,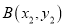 是平面上任意两点,我们可以通过构造直角三角形来求
是平面上任意两点,我们可以通过构造直角三角形来求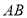 间的距离,如图1,过点
间的距离,如图1,过点 、
、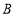 分别向
分别向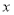 轴、
轴、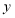 轴作垂线
轴作垂线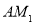 ,
, 和
和 ,
,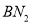 ,垂足分别是
,垂足分别是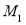 ,
,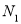 ,
,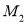 ,
,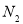 ,直线
,直线 交
交 于点
于点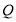 ,在
,在 中,
中,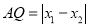 ,
,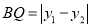 ∴
∴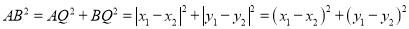 ∴
∴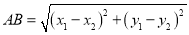 ,我们称此公式
,我们称此公式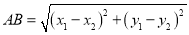 为平面直角坐标系内任意两点
为平面直角坐标系内任意两点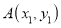 ,
,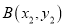 间的距离公式
间的距离公式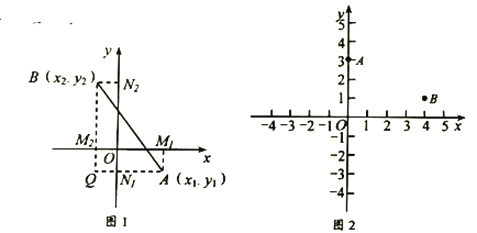
(1)直接应用平面内两点间距离公式计算点
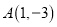 ,
,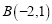 的距离为_________
的距离为_________(2)如图2,已知在平面直角坐标系中有两点
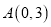 ,
,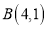 ,
,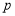 为
为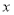 轴上任意一点,求
轴上任意一点,求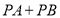 的最小值
的最小值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,经过点A的双曲线y=
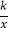 (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.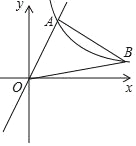
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月25日至27日,第二届“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议。我国准备将
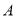 地的茶叶1000吨和
地的茶叶1000吨和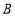 地的茶叶500吨销往“一带一路”沿线的
地的茶叶500吨销往“一带一路”沿线的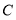 地和
地和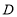 地,
地,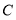 地和
地和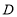 地对茶叶需求分别为900吨和600吨,已知从
地对茶叶需求分别为900吨和600吨,已知从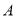 、
、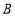 两地运茶叶到
两地运茶叶到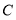 、
、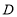 两地的运费(元/吨)如下表所示,设
两地的运费(元/吨)如下表所示,设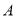 地运到
地运到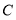 地的茶叶为
地的茶叶为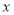 吨,
吨,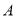
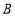
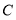
35
40
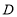
30
45
(1)用含
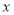 的代数式填空:
的代数式填空: 地运往
地运往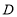 地的茶叶吨数为___________,
地的茶叶吨数为___________,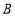 地运往
地运往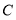 地的茶叶吨数为___________,
地的茶叶吨数为___________,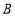 地运往
地运往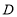 地的茶叶吨数为___________.
地的茶叶吨数为___________.(2)用含
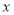 (吨)的代数式表示总运费
(吨)的代数式表示总运费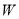 (元),并直接写出自变量
(元),并直接写出自变量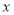 的取值范围;
的取值范围;(3)求最低总运费,并说明总运费最低时的运送方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】情景观察:如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 ,并写出证明过程.
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
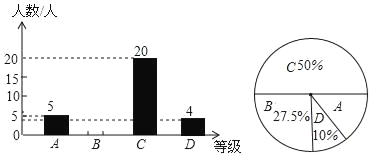
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】服装店10月份以每套500元的进价购进一批羽绒服,当月以标价销售,销售额14000元,进入11月份搞促销活动,每件降价50元,这样销售额比10月份增加了5500元,售出的件数是10月份的1.5倍.
(1)求每件羽绒服的标价是多少元;
(2)进入12月份,该服装店决定把剩余的羽绒服按10月份标价的八折销售,结果全部卖掉,而且这批羽绒服总获利不少于12700元,问这批羽绒服至少购进多少件?
相关试题

