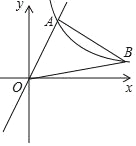
【题目】如图,在平面直角坐标系中,经过点A的双曲线y=![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
参考答案:
【答案】![]()
【解析】分析:过A作AM⊥y轴于M,过B作BD选择x轴于D,直线BD与AM交于点N,则OD=MN,DN=OM,∠AMO=∠BNA=90°,由等腰三角形的判定与性质得出OA=BA,∠OAB=90°,证出∠AOM=∠BAN,由AAS证明△AOM≌△BAN,得出AM=BN=1,OM=AN=k,求出B(1+k,k﹣1),得出方程(1+k)(k﹣1)=k,解方程即可.
详解:如图所示,过A作AM⊥y轴于M,过B作BD选择x轴于D,直线BD与AM交于点N,
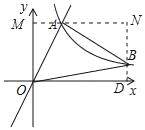
则OD=MN,DN=OM,∠AMO=∠BNA=90°,
∴∠AOM+∠OAM=90°,
∵∠AOB=∠OBA=45°,
∴OA=BA,∠OAB=90°,
∴∠OAM+∠BAN=90°,
∴∠AOM=∠BAN,
∴△AOM≌△BAN,
∴AM=BN=1,OM=AN=k,
∴OD=1+k,BD=OM﹣BN=k﹣1
∴B(1+k,k﹣1),
∵双曲线y=![]() (x>0)经过点B,
(x>0)经过点B,
∴(1+k)(k﹣1)=k,
整理得:k2﹣k﹣1=0,
解得:k=![]() (负值已舍去),
(负值已舍去),
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某医药研究所开发了一种新药,在试验效果时发现,如果成人按规定剂量服用,服药后血液中的含药量逐渐增多,一段时间后达到最大值,接着药量逐步衰减直至血液中含药量为0,每毫升血液中含药量
 (微克)随时间
(微克)随时间 (小时)的变化如图所示,下列说法:(1)2小时血液中含药量最高,达每毫升6微克.(2)每毫升血液中含药量不低于4微克的时间持续达到了6小时.(3)如果一病人下午6:00按规定剂量服此药,那么,第二天中午12:00,血液中不再含有该药,其中正确说法的个数是()
(小时)的变化如图所示,下列说法:(1)2小时血液中含药量最高,达每毫升6微克.(2)每毫升血液中含药量不低于4微克的时间持续达到了6小时.(3)如果一病人下午6:00按规定剂量服此药,那么,第二天中午12:00,血液中不再含有该药,其中正确说法的个数是()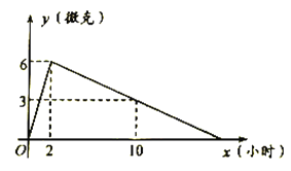
A. 0B. 1
C. 2D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年6月11日至17日是我国第29个全国节能宣传周,主题为“节能减耗,保卫蓝天”。某学校为配合宣传活动,抽查了某班级10天的用电量,数据如下表(单位:度):
度数
8
9
10
13
14
15
天数
1
1
2
3
1
2
(1)这10天用电量的众数是___________,中位数是_________;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,试估计该校6月份(30天)总的用电量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,完成(1)、(2)小题.在平面直角坐标系中,已知
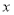 轴上两点
轴上两点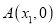 ,
,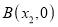 的距离记作
的距离记作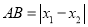 ,如果
,如果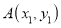 ,
,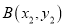 是平面上任意两点,我们可以通过构造直角三角形来求
是平面上任意两点,我们可以通过构造直角三角形来求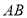 间的距离,如图1,过点
间的距离,如图1,过点 、
、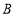 分别向
分别向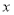 轴、
轴、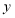 轴作垂线
轴作垂线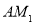 ,
, 和
和 ,
,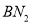 ,垂足分别是
,垂足分别是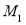 ,
,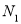 ,
,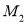 ,
,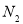 ,直线
,直线 交
交 于点
于点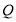 ,在
,在 中,
中,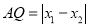 ,
,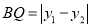 ∴
∴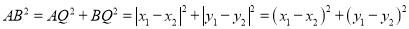 ∴
∴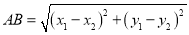 ,我们称此公式
,我们称此公式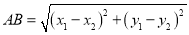 为平面直角坐标系内任意两点
为平面直角坐标系内任意两点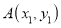 ,
,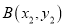 间的距离公式
间的距离公式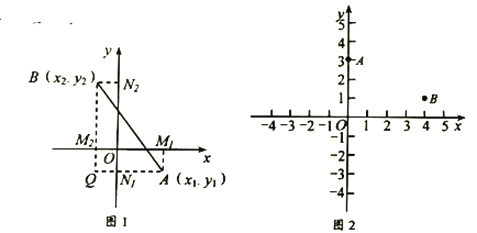
(1)直接应用平面内两点间距离公式计算点
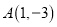 ,
,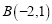 的距离为_________
的距离为_________(2)如图2,已知在平面直角坐标系中有两点
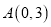 ,
,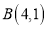 ,
,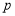 为
为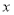 轴上任意一点,求
轴上任意一点,求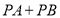 的最小值
的最小值 -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月25日至27日,第二届“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议。我国准备将
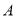 地的茶叶1000吨和
地的茶叶1000吨和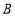 地的茶叶500吨销往“一带一路”沿线的
地的茶叶500吨销往“一带一路”沿线的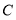 地和
地和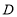 地,
地,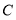 地和
地和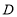 地对茶叶需求分别为900吨和600吨,已知从
地对茶叶需求分别为900吨和600吨,已知从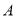 、
、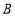 两地运茶叶到
两地运茶叶到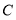 、
、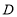 两地的运费(元/吨)如下表所示,设
两地的运费(元/吨)如下表所示,设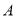 地运到
地运到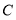 地的茶叶为
地的茶叶为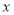 吨,
吨,
35
40
30
45
(1)用含
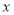 的代数式填空:
的代数式填空: 地运往
地运往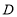 地的茶叶吨数为___________,
地的茶叶吨数为___________,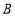 地运往
地运往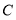 地的茶叶吨数为___________,
地的茶叶吨数为___________,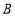 地运往
地运往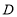 地的茶叶吨数为___________.
地的茶叶吨数为___________.(2)用含
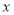 (吨)的代数式表示总运费
(吨)的代数式表示总运费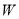 (元),并直接写出自变量
(元),并直接写出自变量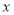 的取值范围;
的取值范围;(3)求最低总运费,并说明总运费最低时的运送方案.
-
科目: 来源: 题型:
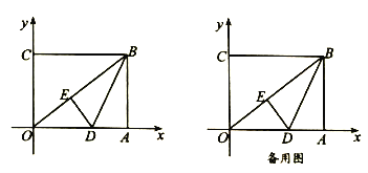
查看答案和解析>>【题目】如图,在平面直角坐标系中,
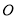 为坐标原点,矩形
为坐标原点,矩形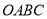 的顶点
的顶点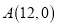 、
、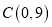 ,将矩形
,将矩形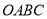 的一个角
的一个角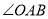 沿直线
沿直线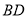 折叠,使得点
折叠,使得点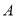 落在对角线
落在对角线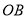 上的点
上的点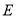 处,折痕与
处,折痕与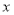 轴交于点
轴交于点 .
.
(1)线段
 的长度为__________;
的长度为__________;(2)求直线
 所对应的函数解析式;
所对应的函数解析式;(3)若点
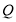 在线段
在线段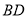 上,在线段
上,在线段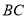 上是否存在点
上是否存在点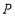 ,使四边形
,使四边形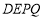 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点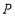 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】情景观察:如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 ,并写出证明过程.
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.

相关试题

