【题目】2019年4月25日至27日,第二届“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议。我国准备将![]() 地的茶叶1000吨和
地的茶叶1000吨和![]() 地的茶叶500吨销往“一带一路”沿线的
地的茶叶500吨销往“一带一路”沿线的![]() 地和
地和![]() 地,
地,![]() 地和
地和![]() 地对茶叶需求分别为900吨和600吨,已知从
地对茶叶需求分别为900吨和600吨,已知从![]() 、
、![]() 两地运茶叶到
两地运茶叶到![]() 、
、![]() 两地的运费(元/吨)如下表所示,设
两地的运费(元/吨)如下表所示,设![]() 地运到
地运到![]() 地的茶叶为
地的茶叶为![]() 吨,
吨,
|
| |
| 35 | 40 |
| 30 | 45 |
(1)用含![]() 的代数式填空:
的代数式填空:![]() 地运往
地运往![]() 地的茶叶吨数为___________,
地的茶叶吨数为___________,![]() 地运往
地运往![]() 地的茶叶吨数为___________,
地的茶叶吨数为___________,![]() 地运往
地运往![]() 地的茶叶吨数为___________.
地的茶叶吨数为___________.
(2)用含![]() (吨)的代数式表示总运费
(吨)的代数式表示总运费![]() (元),并直接写出自变量
(元),并直接写出自变量![]() 的取值范围;
的取值范围;
(3)求最低总运费,并说明总运费最低时的运送方案.
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)由
;(3)由![]() 地运往
地运往![]() 地400吨,运往
地400吨,运往![]() 地600吨;由
地600吨;由![]() 地运往
地运往![]() 地500吨时运费最低
地500吨时运费最低
【解析】
(1)从A地运往C地x吨,A地有1000吨,所以只能运往D地(1000-x)吨;C地需要900吨,那么B地运往C地(900-x),D地需要600吨,那么运往D(x-400)吨;
(2)根据总运费=A地运往C地运费+A地运往D地运费+B地运往C地运费+B地运往D地运费代入数值或字母可得;
(3)根据(2)中得到的一次函数关系式,结合函数的性质和取值范围确定总运费最低方案。
(1)![]() ,
,![]() ,
,![]()
(2)![]()
![]() (
(![]() )
)
(3)∵![]() ,
,
∴![]() 随
随![]() 的增大而增大。
的增大而增大。
∵![]()
∴当![]() 时,
时,![]() 最小
最小![]() .
.
∴由![]() 地运往
地运往![]() 地400吨,运往
地400吨,运往![]() 地600吨;
地600吨;
由![]() 地运往
地运往![]() 地500吨时运费最低。
地500吨时运费最低。
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年6月11日至17日是我国第29个全国节能宣传周,主题为“节能减耗,保卫蓝天”。某学校为配合宣传活动,抽查了某班级10天的用电量,数据如下表(单位:度):
度数
8
9
10
13
14
15
天数
1
1
2
3
1
2
(1)这10天用电量的众数是___________,中位数是_________;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,试估计该校6月份(30天)总的用电量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,完成(1)、(2)小题.在平面直角坐标系中,已知
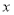 轴上两点
轴上两点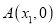 ,
,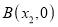 的距离记作
的距离记作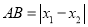 ,如果
,如果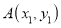 ,
,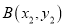 是平面上任意两点,我们可以通过构造直角三角形来求
是平面上任意两点,我们可以通过构造直角三角形来求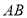 间的距离,如图1,过点
间的距离,如图1,过点 、
、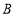 分别向
分别向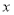 轴、
轴、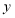 轴作垂线
轴作垂线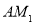 ,
, 和
和 ,
,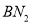 ,垂足分别是
,垂足分别是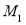 ,
,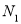 ,
,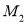 ,
,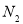 ,直线
,直线 交
交 于点
于点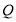 ,在
,在 中,
中,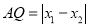 ,
,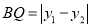 ∴
∴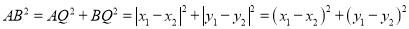 ∴
∴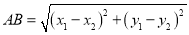 ,我们称此公式
,我们称此公式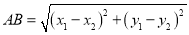 为平面直角坐标系内任意两点
为平面直角坐标系内任意两点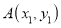 ,
,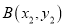 间的距离公式
间的距离公式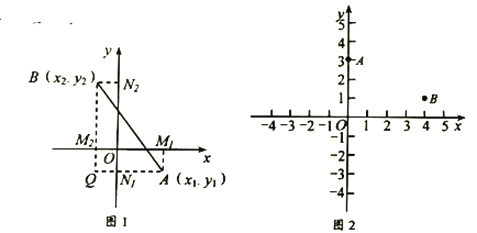
(1)直接应用平面内两点间距离公式计算点
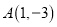 ,
,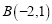 的距离为_________
的距离为_________(2)如图2,已知在平面直角坐标系中有两点
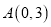 ,
,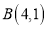 ,
,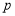 为
为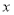 轴上任意一点,求
轴上任意一点,求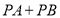 的最小值
的最小值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,经过点A的双曲线y=
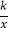 (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.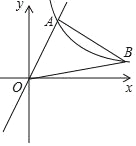
-
科目: 来源: 题型:
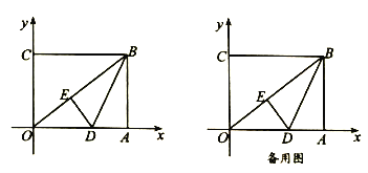
查看答案和解析>>【题目】如图,在平面直角坐标系中,
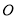 为坐标原点,矩形
为坐标原点,矩形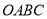 的顶点
的顶点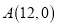 、
、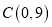 ,将矩形
,将矩形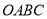 的一个角
的一个角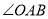 沿直线
沿直线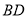 折叠,使得点
折叠,使得点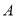 落在对角线
落在对角线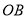 上的点
上的点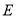 处,折痕与
处,折痕与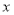 轴交于点
轴交于点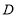 .
.
(1)线段
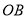 的长度为__________;
的长度为__________;(2)求直线
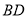 所对应的函数解析式;
所对应的函数解析式;(3)若点
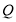 在线段
在线段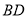 上,在线段
上,在线段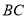 上是否存在点
上是否存在点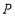 ,使四边形
,使四边形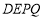 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点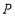 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】情景观察:如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 ,并写出证明过程.
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
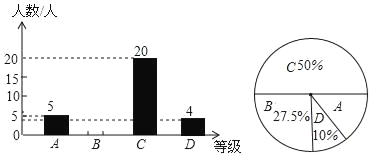
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
相关试题

